题目内容
已知数列{an}满足a1=2,且an+1an+an+1-2an=0,n∈N*,则a2=________;并归纳出数列{an}的通项公式an=________.


分析:将n=1,代入已知等式,结合a1=2可以得到a2的值.再用n=2、3、4、5,求出数列的前面几项,发现各项都是一个分数,它的分子比分母大1,且分子成等比数列的特征,由此可以推出数列{an}的通项公式.
解答:当n=1时,a1a2+a2-2a1=0,结合a1=2,得
2a2+a2-2×2=0?a2=

再取n=2、3、4、5,用同样的方法可以算出:
a3=
 ,a4=
,a4=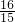 ,a5=
,a5=
所以猜想:

接下来证明此结论:
∵an+1an+an+1-2an=0
∴
 ?
?
∴数列
 构成以
构成以 为首项,公比为
为首项,公比为 的等比数列
的等比数列∴

所以
 ,可得an=
,可得an=
点评:本题以一个数列模型为载体,考查了数列的递推关系、归纳推理和等比数列的通项等知识点,属于中档题.

练习册系列答案
相关题目