题目内容
11.已知f(x)是定义域为R的单调减的奇函数,若f(3x+1)+f(1)≥0,则x的取值范围是$({-∞,-\frac{2}{3}}]$.分析 根据奇函数的性质等价转化所求的不等式,利用函数的单调性列出关于x的不等式,再求出x的取值范围.
解答 解:因为f(x)是定义域为R的奇函数,
所以不等式f(3x+1)+f(1)≥0等价于:f(3x+1)≥f(-1),
因为f(x)是定义域为R的单调减函数,
所以3x+1≤-1,解得x≤$-\frac{2}{3}$,
即x的取值范围是$({-∞,-\frac{2}{3}}]$,
故答案为:$({-∞,-\frac{2}{3}}]$.
点评 本题考查函数的奇偶性、单调性的综合应用,正确转化所求的不等式是解题的关键,考查转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.直线x=t分别与函数f(x)=ex+1的图象及g(x)=2x-1的图象相交于点A和点B,则|AB|的最小值为( )
| A. | 2 | B. | 3 | C. | 4-2ln2 | D. | 3-2ln2 |
6.${(\;{x^2}-\frac{1}{2x}\;)^6}$的展开式中,常数项等于( )
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | $-\frac{15}{16}$ | D. | $\frac{15}{16}$ |
20.函数f(x)的图象向左平移一个单位长度,所得的图象与函数y=2x的图象关于y轴对称,则f(x)=( )
| A. | y=2x-1 | B. | y=${(\frac{1}{2})^{x-1}}$ | C. | y=${(\frac{1}{2})^{x+1}}$ | D. | y=2x+1 |
1.若x+y=1,则sinx+siny与1的大小关系是( )
| A. | sinx+siny>1 | B. | sinx+siny=1 | C. | sinx+siny<1 | D. | 随x、y的值而定 |
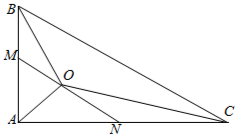 如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].
如图所示,△ABC中,AB⊥AC,AB=6,AC=8.边AB,AC的中点分别为M,N.若O为线段MN上任一点,则$\overrightarrow{OB}•\overrightarrow{OC}+\overrightarrow{OA}•\overrightarrow{OB}+\overrightarrow{OA}•\overrightarrow{OC}$的取值范围是[$-\frac{180}{11},-9$].