题目内容
4.在$[{-\frac{π}{2},π}]$上随机的取一个数x,则事件“满足不等式$|{sinx}|≤\frac{1}{2}$”发生的概率为$\frac{1}{3}$.分析 求出名字条件的x的范围,根据几何概型求出名字条件的概率即可.
解答 解:在$[{-\frac{π}{2},π}]$上,不等式$|{sinx}|≤\frac{1}{2}$”,
解得:-$\frac{π}{6}$≤x≤$\frac{π}{6}$或$\frac{5π}{6}$≤x≤π,
故满足不等式$|{sinx}|≤\frac{1}{2}$”发生的概率:
p=$\frac{\frac{π}{6}-(-\frac{π}{6})+(π-\frac{5π}{6})}{π-(-\frac{π}{2})}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$.
点评 本题考查了几何概型问题,考查三角函数的性质,是一道基础题.

练习册系列答案
相关题目
15.复数z满足(z+2)i=3-2i,则z的共轭复数为( )
| A. | 4+3i | B. | 4-3i | C. | -4+3i | D. | -4-3i |
19.函数$y=sin(2x+\frac{π}{3})$的图象经过下列平移,可以得到函数$y=cos(2x+\frac{π}{6})$图象的是( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
16.下列四条直线,其倾斜角最大的是( )
| A. | x+2y+3=0 | B. | 2x-y+1=0 | C. | x+y+1=0 | D. | x+1=0 |
13.命题p:若a>b,则ac2>bc2;命题q:?x0>0,使得x0-1+lnx0=0,则下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∨(¬q) | D. | (¬p)∧(¬q) |
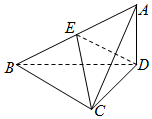 已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.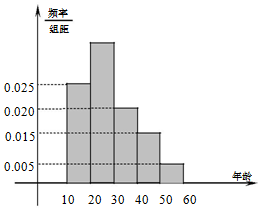 •滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.
•滑雪场开业当天共有 500 人滑雪,滑雪服务中心根据他们的年龄分成[10,20),[20,30),[30,40),[40,50),[50,60]五个组,现按照分层抽样的方法选取 20 人参加有奖活动,这些人的样本数据的频率分布直方图如下图所示,从左往右分别为一组、二组、三组、四组、五组.