题目内容
已知函数f(x)=(ax2+x-1)ex其中e是自然对数的底数a∈R.
(1)若a=1,求曲线f(x)在点(1,f(1))处的切线方程;
(2)若a<0,求f(x)的单调区间;
(3)若a=-1,函数f(x)的图象与函数g(x)=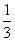 x3+
x3+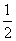 x2+m的图象有3个不同的交点,求实数m的取值范围.
x2+m的图象有3个不同的交点,求实数m的取值范围.
(1)a=1时,f(x)=(x2+x-1)ex,
所以f′(x)=(2x+1)ex+(x2+x-1)ex=(x2+3x)ex,
所以曲线f(x)在点(1,f(1))处的切线斜率为k=f′(1)=4e.
又因为f(1)=e,
所以所求切线方程为y-e=4e(x-1),即4ex-y-3e=0.
(2)f′(x)=(2ax+1)ex+(ax2+x-1)ex=[ax2+(2a+1)x]ex,
①若-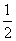 <a<0,当x<0或x>-
<a<0,当x<0或x>-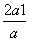 时,f′(x)<0;
时,f′(x)<0;
当0<x<-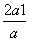 时,f′(x)>0.
时,f′(x)>0.
所以f(x)的单调递减区间为(-∞,0],[-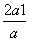 ,+∞);单调递增区间为[0,-
,+∞);单调递增区间为[0,-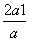 ].
].
②若a=-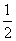 ,则f′(x)=-
,则f′(x)=-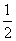 x2ex≤0,所以f(x)的单调递减区间为(-∞,+∞).
x2ex≤0,所以f(x)的单调递减区间为(-∞,+∞).
③若a<-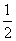 ,当x<-
,当x<-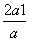 或x>0时,f′(x)<0;
或x>0时,f′(x)<0;
当-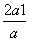 <x<0时,f′(x)>0.
<x<0时,f′(x)>0.


练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 的取值如下表所示:
的取值如下表所示:

 ,则a的值为__________。
,则a的值为__________。 . cos
. cos

 ,(
,( 、
、 、
、 是两两不等的常数),
是两两不等的常数), .
. 的正三角形ABC中,设
的正三角形ABC中,设 =c,
=c,  =a,
=a,  =b,则a·b+b·c+c·a等于_______________
=b,则a·b+b·c+c·a等于_______________  ,则
,则 __________.
__________.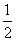 ,在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是
,在第一次闭合出现红灯的条件下第二次闭合还出现红灯的概率是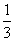 ,则两次闭合都出现红灯的概率为………………………………………( )
,则两次闭合都出现红灯的概率为………………………………………( )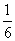 B.
B.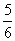 C.
C.