题目内容
已知曲线C上动点P(x，y)到定点F1(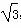
，0)与定直线l1∶x＝
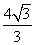的距离之比为常数
.
(1) 求曲线C的轨迹方程；
(2) 以曲线C的左顶点T为圆心作圆T：(x＋2)2＋y2＝r2(r>0)，设圆T与曲线C交于点M与点N，求
·
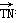的最小值，并求此时圆T的方程．
解：(1) 过点P作直线的垂线，垂足为D.
＝，
所以该曲线的方程为
＋y2＝1.
(2) 点M与点N关于x轴对称，设M(x1，y1)，N(x1，－y1)，不妨设y1>0.由于点M在椭圆C上，所以y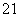
＝1－
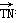.由已知T(－2，0)，则＝(x1＋2，y1)，＝(x1＋2，－y1)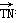，∴ ·＝(x1＋2，y1)·(x1＋2，－y1)＝(x1＋2)2－y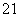＝(x1＋2)2－
＝
x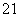＋4x1＋3＝·
－
.由于－2<x1<2，故当x1＝－
时，
·
取得最小值为－.计算得，y1＝
，故M
.
又点M在圆T上，代入圆的方程得到r2＝
.
故圆T的方程为(x＋2)2＋y2＝.
练习册系列答案
应用题作业本系列答案
相关题目
＝________．
－
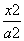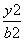＝1的离心率为2，焦点到渐近线的距离等于
，过右焦点F2的直线l交双曲线于A、B两点，F1为左焦点．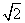
，求直线l的方程．
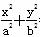＝1(a>b>0，a、b为常数)，动圆C1：x2＋y2＝t
与C0相交于A′，B′，C′，D′四点，其中b<t2<a，t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等，证明：t
上的点．若F1、F2是椭圆的两个焦点，则
＝________．
·
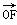＝1.设|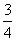
c.若以O为中心，F为一个焦点的椭圆经过点Q，当
取最小值时，求椭圆的方程．