题目内容
19.若不论m取何实数,直线l:mx+y-1+2m=0恒过一定点,则该定点的坐标是(-2,1).分析 将直线的方程整理成直线系的标准形式,求两定直线的交点,此点即为直线恒过的定点.
解答 解:直线l:mx+y-1+2m=0可化为m(x+2)+(y-1)=0
由题意,可得$\left\{\begin{array}{l}{x+2=0}\\{y-1=0}\end{array}\right.$,
∴x=-2,y=1,
∴直线l:mx+y-1+2m=0恒过一定点(-2,1).
故答案为(-2,1).
点评 本题重点考查直线恒过定点问题,将方程恰当变形,构建方程组是解题的关键.

练习册系列答案
相关题目
7.对任意x∈R,函数f(x)的导数存在,若f'(x)>f(x),则以下正确的是( )
| A. | f(2015)>f(0) | B. | f(2015)<f(0) | C. | f(2015)>e2015•f(0) | D. | f(2015)<e2015•f(0) |
11.已知函数$f(x)=\left\{{{\;}_{{3^x},x≤0}^{{{log}_2}x,x>0}}\right.$,则$f[{f(\frac{1}{2})}]$=( )
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 在小时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2015时对应的指头是中指.(填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).
在小时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2015时对应的指头是中指.(填出指头的名称,各指头的名称依次为大拇指、食指、中指、无名指、小指).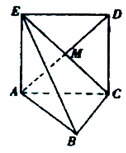 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC