题目内容
在锐角 中,
中,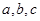 分别是内角
分别是内角 所对边长,且满足
所对边长,且满足 .
.
(1)求角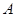 的大小;
的大小;
(2)若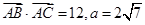 ,求
,求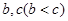 .
.
(1) ;(2)
;(2) ,
, .
.
解析试题分析:(1)先利用题中的等式进行化简,并计算出 的值,利用
的值,利用 为锐角三角形这一条件求出角
为锐角三角形这一条件求出角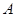 的大小;(2)先将
的大小;(2)先将 表示为
表示为 ,然后利用余弦定理
,然后利用余弦定理 这两个方程求出
这两个方程求出 与
与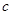 的值.
的值.
试题解析:(1)
 ,
, 为锐角三角形,所以
为锐角三角形,所以 ,故
,故 ;
;
(2) ,所以
,所以 ,
,
由余弦定理得 ,所以
,所以 ,
,
于是有 ,解得
,解得 ,
, .
.
考点:1.平面向量的数量积;2.余弦定理;3.两角和与差的三角函数

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
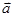 =(cos
=(cos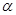 ,sin
,sin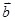 =(cos
=(cos ,sin
,sin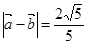 。
。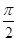 ,-
,-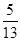 ,求sin
,求sin
 求(1)
求(1) ;(2)
;(2) .
.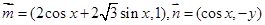 ,且
,且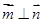 .
.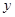 表示为
表示为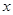 的函数
的函数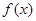 ,并求
,并求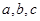 分别为
分别为 的三个内角
的三个内角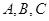 对应的边长,若
对应的边长,若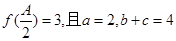 ,求
,求
 ,
, ,求
,求
 ,若
,若 ,求
,求 的值.
的值. 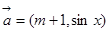 ,
,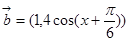 ,设函数
,设函数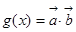 ,(
,(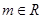 ,且
,且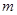 为常数)
为常数)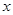 为任意实数,求
为任意实数,求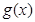 的最小正周期;
的最小正周期; 上的最大值与最小值之和为
上的最大值与最小值之和为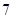 ,求
,求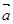 、
、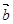 、
、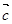 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中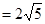 ,且
,且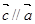 ,求
,求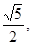 且
且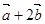 与
与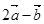 垂直,求
垂直,求 .
. ,
, ,
, 与
与 、
、 的夹角相等,且
的夹角相等,且 ,求向量
,求向量