Question

已知＝(2asin2x，a)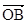，＝(－1,2sinxcosx＋1)，O为坐标原点，a≠0，设f(x)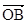＝·＋b，b>a。

(1)若a>0，写出函数y＝f(x)的单调递增区间；

(2)若函数y＝f(x)的定义域为[，π]，值域为[2,5]，求实数a与b的值。

 

Answer 1

【答案】

(1)f(x)＝－2asin2x＋2asinxcosx＋a＋b＝2asin＋b，       2分

∵a>0，

∴由2kπ－≤2x＋≤2kπ＋得，

kπ－≤x≤kπ＋，k∈Z.                                    5分

∴函数y＝f(x)的单调递增区间是[kπ－，kπ＋](k∈Z)           6分

(2)x∈[，π]时，2x＋∈[，]，                             8分

sin∈[－1，]                                       10分

当a>0时，f(x)∈[－2a＋b，a＋b]

∴，得，                               12分

当a<0时，f(x)∈[a＋b，－2a＋b]

∴，得                               14分

综上知，或                                 16分

 

【解析】略