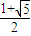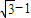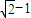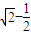题目内容
已知点A是椭圆 上一点,F为椭圆的一个焦点,且AF⊥x轴,|AF|=焦距,则椭圆的离心率是
上一点,F为椭圆的一个焦点,且AF⊥x轴,|AF|=焦距,则椭圆的离心率是
- A.

- B.

- C.

- D.
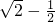
C
分析:通过焦点F的横坐标,代入椭圆方程,求出A的纵坐标,利用|AF|=焦距,结合椭圆中a,b,c的关系,求出椭圆的离心率.
解答:设F为椭圆的右焦点,且AF⊥x轴,所以F(c,0),则 ,解得y=±
,解得y=± ,
,
因为,|AF|=焦距,所以 ,即b2=2ac,a2-c2=2ac,
,即b2=2ac,a2-c2=2ac,
∴e2+2e-1=0,解得e= 或e=-
或e=- (舍去)
(舍去)
故选C.
点评:本题考查椭圆的基本性质,考查计算能力,基本知识的掌握程度决定解题的质量与速度.
分析:通过焦点F的横坐标,代入椭圆方程,求出A的纵坐标,利用|AF|=焦距,结合椭圆中a,b,c的关系,求出椭圆的离心率.
解答:设F为椭圆的右焦点,且AF⊥x轴,所以F(c,0),则
 ,解得y=±
,解得y=± ,
,因为,|AF|=焦距,所以
 ,即b2=2ac,a2-c2=2ac,
,即b2=2ac,a2-c2=2ac,∴e2+2e-1=0,解得e=
 或e=-
或e=- (舍去)
(舍去)故选C.
点评:本题考查椭圆的基本性质,考查计算能力,基本知识的掌握程度决定解题的质量与速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上一点,F1,F2分别为椭圆的左、右焦点,M为△PF1F2的内心,若
上一点,F1,F2分别为椭圆的左、右焦点,M为△PF1F2的内心,若 =
= -
- 成立,则λ的值为 ( )
成立,则λ的值为 ( )



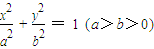 上一点,F为椭圆的一个焦点,且AF⊥x轴,|AF|=焦距,则椭圆的离心率是( )
上一点,F为椭圆的一个焦点,且AF⊥x轴,|AF|=焦距,则椭圆的离心率是( )