题目内容
已知不等式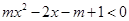
，
（1）若对所有的实数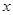
不等式恒成立，求
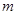的取值范围；
（2）设不等式对于满足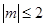
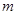的一切的值都成立，求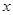的取值范围。
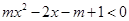，（1）若对所有的实数
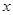不等式恒成立，求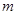的取值范围；（2）设不等式对于满足
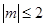的一切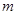的值都成立，求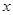的取值范围。（1）不存在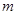使不等式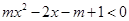恒成立（2）
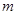使不等式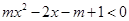恒成立（2）试题分析：（1）当
时，
，不恒成立当
时，设
，不等式
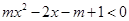，若对所有的实数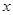不等式恒成立，即二次函数
图象全在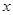轴的下方所以
，且
，无解综上，不存在这样的
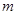，使不等式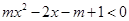，若对所有的实数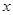不等式恒成立（2）设
，即
解得：
，所以
综上，
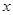的取值范围是点评：在不等式恒成立中转化为与之对应的函数值域的范围，进而结合函数图像得到满足的条件，需要对比注意的是两小题自变量的值是不一样的
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
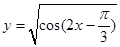的定义域是 .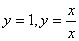 
%，则销售量将减少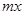
%，且该化工产品每吨的价格上涨幅度不超过
%，
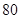其中
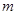为正常数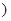
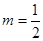时，该产品每吨的价格上涨百分之几，可使销售的总金额最大？
（
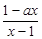）为奇函数，a为常数．
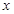的值，不等式
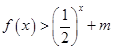恒成立，求实数
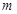的取值范围.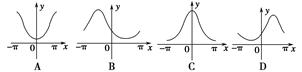
的图象大致是
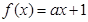在R上递减，则函数
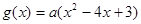的增区间是 ( )
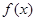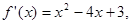的导函数
则函数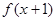
的单调递减区间是（ ）