题目内容
设f(x)=log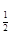 (
(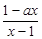 )为奇函数,a为常数.
)为奇函数,a为常数.
(Ⅰ)求a的值;
(Ⅱ)证明f(x)在(1,+∞)内单调递增;
(Ⅲ)若对于[3,4]上的每一个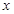 的值,不等式
的值,不等式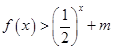 恒成立,求实数
恒成立,求实数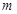 的取值范围.
的取值范围.
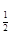 (
(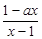 )为奇函数,a为常数.
)为奇函数,a为常数.(Ⅰ)求a的值;
(Ⅱ)证明f(x)在(1,+∞)内单调递增;
(Ⅲ)若对于[3,4]上的每一个
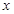 的值,不等式
的值,不等式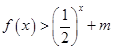 恒成立,求实数
恒成立,求实数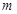 的取值范围.
的取值范围.(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅲ)
(Ⅲ)
 (Ⅱ)
(Ⅱ)
 (Ⅲ)
(Ⅲ)
试题分析:(Ⅰ)函数是奇函数,所以
 带入得
带入得 ,经验证
,经验证 时不合题意
时不合题意


点评:函数是奇函数则满足
 ,复合函数的单调性由构成复合函数的基本初等函数决定,当两初等函数单调性相同时,复合后递增,反之递减;不等式恒成立求参数范围的题目常采用分离参数法转化为求函数最值的题目
,复合函数的单调性由构成复合函数的基本初等函数决定,当两初等函数单调性相同时,复合后递增,反之递减;不等式恒成立求参数范围的题目常采用分离参数法转化为求函数最值的题目
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
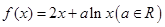 .
.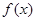 的单调性;
的单调性;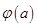 ,求
,求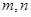 为
为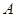 内的任意两个值,试比较
内的任意两个值,试比较 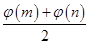 与
与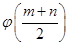 的大小.
的大小.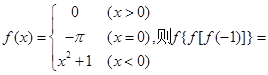
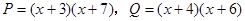 ,则P,Q的大小关系为
,则P,Q的大小关系为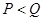
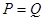
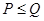
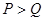
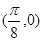 为函数
为函数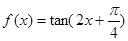 的一个对称中心
的一个对称中心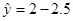 x,当变量x增加一个单位时,y大约减少2.5个单位
x,当变量x增加一个单位时,y大约减少2.5个单位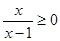 ”则
”则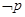 “
“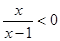 ”
”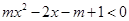 ,
,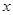 不等式恒成立,求
不等式恒成立,求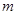 的取值范围;
的取值范围;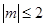 的一切
的一切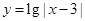 和
和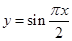
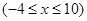 ,下列说法正确的是 .
,下列说法正确的是 .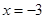 对称;
对称;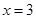 对称;
对称;
 在区间
在区间 上的最值.
上的最值.