题目内容
6．有一段演绎推理：“直线平行于平面，则平行于平面内所有直线；已知直线a?平面α，直线b∥平面α，则b∥a”的结论显然是错误的，这是因为（ ）| A． | 大前提错误 | B． | 小前提错误 | C． | 推理形式错误 | D． | 非以上错误 |
分析 分析该演绎推理的三段论，即可得出错误的原因是什么．
解答 解：该演绎推理的大前提是：若直线平行于平面，则该直线平行于平面内所有直线；
小前提是：已知直线b∥平面α，直线a?平面α；
结论是：直线b∥直线a；
该结论是错误的，因为大前提是错误的，
正确叙述是“若直线平行于平面，过该直线作平面与已知平面相交，则交线与该直线平行”．
故选：A．
点评 本题通过演绎推理的三段论叙述，考查了空间中线面垂直的性质定理的应用问题，是基础题．
练习册系列答案
相关题目
16．已知p：x2-4x-5＞0，q：x2-2x+1-λ2＞0，若p是q的充分不必要条件，则正实数λ的取值范围是（ ）
| A． | （0，1] | B． | （0，2） | C． | $（{0，\frac{3}{2}}]$ | D． | （0，2] |
17．巴西世界杯足球赛正在如火如荼进行．某人为了了解我校学生“通过电视收看世界杯”是否与性别有关，从全校学生中随机抽取30名学生进行了问卷调查，得到了如下列联表：
已知在这30名同学中随机抽取1人，抽到“通过电视收看世界杯”的学生的概率是$\frac{8}{15}$．
（I）请将上面的列联表补充完整，并据此资料分析在犯错误概率不超过0.01的前提下“通过电视收看世界杯”与性别是否有关？
（II）若从这30名同学中的男同学中随机抽取2人参加一活动，记“通过电视收看世界杯”的人数为X，求X的分布列和均值．
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（c+a）（b+d）}$，n=a+b+c+d）
| 男生 | 女生 | 合计 | |
| 收看 | 10 | ||
| 不收看 | 8 | ||
| 合计 | 30 |
（I）请将上面的列联表补充完整，并据此资料分析在犯错误概率不超过0.01的前提下“通过电视收看世界杯”与性别是否有关？
（II）若从这30名同学中的男同学中随机抽取2人参加一活动，记“通过电视收看世界杯”的人数为X，求X的分布列和均值．
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（c+a）（b+d）}$，n=a+b+c+d）
| P（K2＞k0） | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
14．已知在映射f下，（x，y）的象是（x+y，x-y），则元素（3，1）的原象为（ ）
| A． | （1，2） | B． | （2，1） | C． | （-1，2） | D． | （-2，-1） |
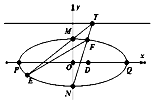已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的上顶点M与左、右焦点F1，F2构成三角形MF1F2面积为$\sqrt{3}$，又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$，左右顶点分别为P，Q．
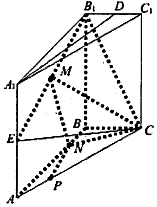已知在三棱柱ABC-A1B1C1中，B1B⊥平面ABC，∠ABC=90°，B1B=AB=2BC=4，D、E分别是B1C1，A1A的中点．