Question

已知定点F为(0,a)(a≠0),点P、M分别在x、y轴上,满足·=0,点N满足+=0.

(1)求N点的轨迹方程C;

(2)过F作一条斜率为k的直线l,l与曲线C交于A、B两点,设G(0,-a),∠AGB=θ,求证:0＜θ≤.

Answer 1

(1)解:∵+=0,

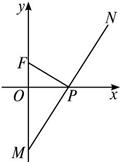
∴P为MN的中点.

设N(x,y),则M(0,-y),P(,0).

于是=(,-a), =(,y).

∵·=0,∴()²-ay=0,

即N点的轨迹方程为x²=4ay.                                       

(2)证明:由题意知直线l的方程为y=kx+a,代入x²=4ay,得x²-4akx-4a²=0.

设A(x₁,y₁),B(x₂,y₂),则x₁+x₂=4ak,x₁x₂=-4a².                              

∴y₁+y₂=(kx₁+a)+(kx₂+a)=k(x₁+x₂)+2a=4ak²+2a,

y₁y₂=(kx₁+a)(kx₂+a)=k²x₁x₂+ak(x₁+x₂)+a²=-4a²k²+4a²k²+a²=a².             

∵G(0,-a),

∴=(x₁,y₁+a),=(x₂,y₂+a).

∴·=x₁x₂+(y₁+a)(y₂+a)=x₁x₂+y₁y₂+a(y₁+y₂)+a²=-4a²+a²+a(4ak²+2a)+a²=4a²k²≥0,

即||||cosθ≥0.

∴cosθ≥0.故0≤θ≤.                                           

又点G(0,-a)不在直线l上,∴A、B、G三点不共线.故0＜θ≤.