题目内容
已知定点F(2,0)和定直线 ,动圆P过定点F与定直线相切,记动圆圆心P的轨迹为曲线C
,动圆P过定点F与定直线相切,记动圆圆心P的轨迹为曲线C
(1)求曲线C的方程.
(2)若以M(2,3)为圆心的圆与抛物线交于A、B不同两点,且线段AB是此圆的直径时,求直线AB的方程
【答案】
(1)  ;(2)
;(2) .
.
【解析】
试题分析:(1)由题意知,P到F的距离等于P到的距离,所以P的轨迹C是以F为焦点,直线 为准线的抛物线,故直接利用抛物线的标准方程写出曲线C的方程;(2)依题意,实质上是已知抛物线的弦AB中点为
为准线的抛物线,故直接利用抛物线的标准方程写出曲线C的方程;(2)依题意,实质上是已知抛物线的弦AB中点为 ,求直线AB的方程,一般方法是设
,求直线AB的方程,一般方法是设 ,代入抛物线方程得
,代入抛物线方程得 ,
, ,两式相减得
,两式相减得 ,即
,即 ,这就是直线AB的斜率.下面就可很方便求出直线AB的方程了.
,这就是直线AB的斜率.下面就可很方便求出直线AB的方程了.
试题解析:(1)由题意知,P到F的距离等于P到的距离,所以P的轨迹C是以F为焦点,直线 为准线的抛物线,它的方程为
为准线的抛物线,它的方程为 5分
5分
(2)设
则
 7分
7分
由AB为圆M 的直径知,
的直径知, 9分
9分
故直线的斜率为 10分
10分
直线AB的方程为
即 12分
12分
考点:(1)抛物线的定义;(2)已知抛物线的弦中点问题.

练习册系列答案
相关题目
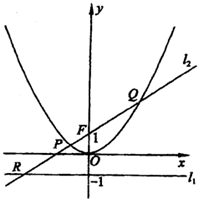 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.