题目内容
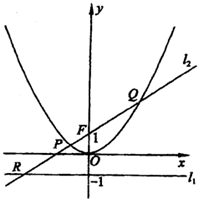
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
(1)求动点C的轨迹方程;
(2)若A,B是所求轨迹上的两个点,满足OA⊥OB(0为坐标原点),求证:直线AB经过一个定点.
(3)过点F的直线l2交轨迹于两点P、Q,交直线l1于点R,求
•
的最小值.
(1)求动点C的轨迹方程;
(2)若A,B是所求轨迹上的两个点,满足OA⊥OB(0为坐标原点),求证:直线AB经过一个定点.
(3)过点F的直线l2交轨迹于两点P、Q,交直线l1于点R,求
| RP |
| RQ |
分析:(1)根据点C到点F的距离等于它到l1的距离,依据抛物线的定义可知点C的轨迹是以F为焦点,l1为准线的抛物线,进而求得其轨迹方程;
(2)设直线AB的方程为y=kx+b代入抛物线方程,利用OA⊥OB,可得x1x2+y1y2=0,即可得到结论;
(3)设出直线l2的方程与抛物线方程联立消去y,设出P,Q的坐标,根据韦达定理表示出x1+x2和x1x2的表达式,进而可得点R的坐标,表示出
•
,根据均值不等式求得其最小值.
(2)设直线AB的方程为y=kx+b代入抛物线方程,利用OA⊥OB,可得x1x2+y1y2=0,即可得到结论;
(3)设出直线l2的方程与抛物线方程联立消去y,设出P,Q的坐标,根据韦达定理表示出x1+x2和x1x2的表达式,进而可得点R的坐标,表示出
| RP |
| RQ |
解答:(1)解:由题设点C到点F的距离等于它到l1的距离,
∴点C的轨迹是以F为焦点,l1为准线的抛物线.
∴所求轨迹的方程为x2=4y.
(2)证明:由已知,设直线AB的方程为y=kx+b代入抛物线方程x2=4y,并整理得x2-4kx-4b=0
设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4b,
因为OA⊥OB,所以x1x2+y1y2=0,即b2-4b=0,解得,b=4或b=0(舍去),
所以直线AB过定点(0,4).
(3)解:由题意直线l2的方程为y=kx+1,与抛物线方程联立消去y,得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则x1+x2=4k,x1x2=-4.
∵直线PQ的斜率k≠0,易得点R的坐标为(-
,-1),
•
=(x1+
)(x2+
)+(kx1+2)(kx2+2)
=(1+k2)x1x2+(
+2k)(x1+x2)+
+4
=-4(1+k2)+4k(
+2k)+
+4=4(k2+
)+8,
∵k2+
≥2,当且仅当k2=1时取到等号.
∴
•
≥4×2+8=16,即
•
的最小值为16.
∴点C的轨迹是以F为焦点,l1为准线的抛物线.
∴所求轨迹的方程为x2=4y.
(2)证明:由已知,设直线AB的方程为y=kx+b代入抛物线方程x2=4y,并整理得x2-4kx-4b=0
设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=-4b,
因为OA⊥OB,所以x1x2+y1y2=0,即b2-4b=0,解得,b=4或b=0(舍去),
所以直线AB过定点(0,4).
(3)解:由题意直线l2的方程为y=kx+1,与抛物线方程联立消去y,得x2-4kx-4=0.
记P(x1,y1),Q(x2,y2),则x1+x2=4k,x1x2=-4.
∵直线PQ的斜率k≠0,易得点R的坐标为(-
| 2 |
| k |
| RP |
| RQ |
| 2 |
| k |
| 2 |
| k |
=(1+k2)x1x2+(
| 2 |
| k |
| 4 |
| k2 |
=-4(1+k2)+4k(
| 2 |
| k |
| 4 |
| k2 |
| 1 |
| k2 |
∵k2+
| 1 |
| k2 |
∴
| RP |
| RQ |
| RP |
| RQ |
点评:本题主要考查了直线与圆锥曲线的关系,考查抛物线方程的求解,考查向量知识的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.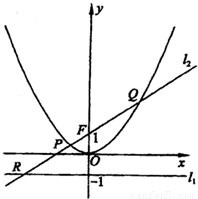 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.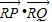 的最小值.
的最小值.