题目内容
12.设m是实数,若x∈R时,不等式|x-m|-|x-1|≤1恒成立,则m的取值范围是[0,2].分析 由绝对值三角不等式,可得|x-m|-|x-1|≤|m-1|,再根据|m-1|≤1求得m的取值范围.
解答 解:∵|x-m|-|x-1|≤|(x-m)-(x-1)|=|m-1|,
故由不等式|x-m|-|x-1|≤1恒成立,可得|m-1|≤1,∴-1≤m-1≤1,
求得0≤m≤2,
故答案为:[0,2].
点评 本题主要考查绝对值三角不等式,绝对值不等式的解法,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
3.执行如图所示的程序框图,则输出S的值是( )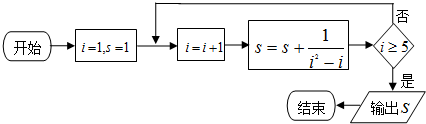

| A. | $\frac{4}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{11}{6}$ |
17.执行如图的程序框图,若输入的x为6,则输出的y的值为( )


| A. | 6 | B. | 4 | C. | 3 | D. | 2.5 |
20.抛物线y=-4x2的准线方程为( )
| A. | x=1 | B. | y=1 | C. | x=$\frac{1}{16}$ | D. | y=$\frac{1}{16}$ |
 铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器,扇形的圆心角α多大时,容器的容积最大?
铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器,扇形的圆心角α多大时,容器的容积最大?