题目内容
5.已知A(a,0),B(3,2+a),直线y=$\frac{1}{2}$ax与线段AB交于M,且$\overrightarrow{AM}$=2$\overrightarrow{MB}$,则a等于2或-4.分析 求出M的坐标代入直线方程解出a.
解答 解:∵$\overrightarrow{AM}$=2$\overrightarrow{MB}$,∴M是AB靠近B的三等分点.
∴M(2+$\frac{a}{3}$,$\frac{4+2a}{3}$).
∵M在直线y=$\frac{1}{2}ax$上,
∴$\frac{4+2a}{3}=\frac{1}{2}a(2+\frac{a}{3})$,解得a=2或a=-4.
故答案为2或-4.
点评 本题考查了平面向量数乘的几何意义,属于基础题.

练习册系列答案
相关题目
13.已知{an}满足a1=1,a2=1,an+2-an+1-an=0,x1,x2是方程x2=x+1两根.求证:
(1)数列{an+1-x1an},和{an+1-x2an}均为等比数列.
(2)求an=?
(1)数列{an+1-x1an},和{an+1-x2an}均为等比数列.
(2)求an=?
10.已知集合A={x|x2-4x<0},B={x|-1≤x≤1},则A∪B=( )
| A. | [-1,1] | B. | [-1,4) | C. | (0,1] | D. | (0,4) |
17.已知集合A={x|y=$\sqrt{4x-x^2}$},B={x||x|≤2},则A∪B=( )
| A. | [-2,2] | B. | [-2,4] | C. | [0,2] | D. | [0,4] |
2.已知等差数列{an}的前n项和为Sn,公差为d,若$\frac{{S}_{2016}}{2016}$-$\frac{{S}_{16}}{16}$=100,则d的值为( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
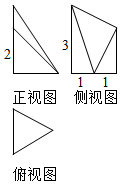 某多面体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角梯形,则该多面体的表面积为10+$\sqrt{3}$+$\sqrt{10}$,体积为$\frac{5\sqrt{3}}{3}$.
某多面体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角梯形,则该多面体的表面积为10+$\sqrt{3}$+$\sqrt{10}$,体积为$\frac{5\sqrt{3}}{3}$.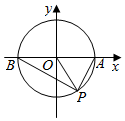 如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.
如图,在平面直角坐标系xOy中,单位圆与x轴的正半轴与负半轴分别交于点A,B,角α的始边为OA,终边与单位圆交于x轴下方一点P.