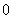题目内容
如图,在四棱锥 中,
中,  为
为 上一点,
上一点,
 平面
平面 .
. ,
, ,
, ,
, ,
,
 为
为 上一点,且
上一点,且 .
.
(Ⅰ) 求证: ;
;
(Ⅱ)若二面角 为
为 ,
,
求 的值.
的值.
 |
(Ⅰ) 证明:连接AC交BE于点M,
连接 .由
.由





(Ⅱ)连 ,过
,过 作
作 于
于 .由于
.由于 ,故
,故 .
.
过 作
作 于
于 ,连
,连 .则
.则 ,即
,即 为二面角
为二面角
 的平面角.
的平面角. 
 ,
,


解法二:以 为坐标原点,
为坐标原点, 为
为 轴建立空间直角坐标系.
轴建立空间直角坐标系.

 ,
, 
设平面 的法向量
的法向量 ,由
,由
 得
得

面 法向量为
法向量为 .
.
由于 , 解得
, 解得 .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,
, ,则公差
,则公差 ______;
______; ______.
______.  与圆
与圆 相交于
相交于 ,
, 两点,若
两点,若 ,则实数
,则实数 的值
的值 都是正实数,且满足
都是正实数,且满足 ,则
,则 的最小值为
的最小值为 中,
中, 分别为角
分别为角 的对边,若
的对边,若 ,且
,且 ,则
,则 的值为 .
的值为 . 时,函数
时,函数 的值恒大于1,则实数
的值恒大于1,则实数 的取值范围是 .
的取值范围是 . 的准线与直线
的准线与直线 之间的距离为3,则该抛物线的方程为 .
之间的距离为3,则该抛物线的方程为 . 则不等式
则不等式 的解集为_______.
的解集为_______.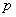 为假命题,命题
为假命题,命题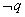 为假命题,则命题“
为假命题,则命题“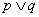 ”为假命题;
”为假命题;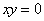 ,则
,则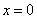 或
或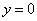 ”的否命题为“若
”的否命题为“若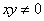 ,则
,则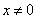 或
或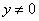 ”;
”;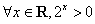 ”的否定是“
”的否定是“ 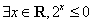 ”.则以上结论正确的个数为
”.则以上结论正确的个数为 B.
B. C.
C. D.
D.