题目内容
13.数列{an}中,a1=1,$\frac{2}{{a}_{n}}$=$\frac{1}{{a}_{n+1}}+\frac{1}{{a}_{n-1}}$(n≥2,n∈N),a5=-11,则其通项为an=$\frac{11}{14-3n}$(n∈N+).分析 由题意可得数列{$\frac{1}{{a}_{n}}$}是以1为首项的等差数列,再求出公差d,即可求得an.
解答 解:∵a1=1,
∴$\frac{1}{{a}_{1}}$=1,
∵$\frac{2}{{a}_{n}}$=$\frac{1}{{a}_{n+1}}+\frac{1}{{a}_{n-1}}$(n≥2),
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项的等差数列,
∵a5=-11,
∴$\frac{1}{{a}_{5}}$=-$\frac{1}{11}$,
设数列{$\frac{1}{{a}_{n}}$}的公差为d,
∴$\frac{1}{{a}_{5}}$=$\frac{1}{{a}_{1}}$+4d,
∴-$\frac{1}{11}$=1+4d,
解得d=-$\frac{3}{11}$,
∴$\frac{1}{{a}_{n}}$=1-$\frac{3}{11}$(n-1),
∴an=$\frac{11}{14-3n}$,
当n=1时,a1=1成立,
综上所述其通项为an=$\frac{11}{14-3n}$,( n∈N+ )
故答案为:an=$\frac{11}{14-3n}$,( n∈N* )
点评 本题主要考查用构造法求数列的通项公式,判断数列{$\frac{1}{{a}_{n}}$}是以1为首项的等差数列是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知tanα=$\frac{1}{2}$,则$\frac{tan(\frac{π}{4}+α)-1}{1+tan(\frac{π}{4}+α)}$的值是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | -3 |
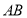 是
是 的直径,
的直径,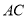 是
是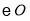 的切线,
的切线, 交
交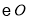 于点
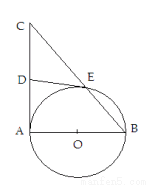
于点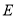 .
.
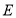 做
做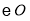 的切线,交
的切线,交 ,证明:
,证明: 是
是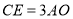 ,求
,求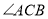 的大小.
的大小. 时,函数
时,函数 取得最大值,则
取得最大值,则 __________.
__________.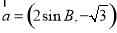 ,
, 且
且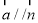 .
.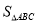 的最大值.
的最大值. ,
, ,则集合
,则集合 =( )
=( )
 B.
B. C.
C. D.R
D.R