题目内容
19.已知α,β都是锐角,sinα=$\frac{1}{2}$,cosβ=$\frac{1}{2}$,则cos(α-β)=$\frac{\sqrt{3}}{2}$.分析 直接求出α,β,然后求解cos(α-β).
解答 解:α,β都是锐角,sinα=$\frac{1}{2}$,cosβ=$\frac{1}{2}$,
α=$\frac{π}{6}$,β=$\frac{π}{3}$,
cos(α-β)=cos($\frac{π}{6}-\frac{π}{3}$)=cos$\frac{π}{6}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{3}}}{2}$.
点评 本题考查三角函数的化简求值,可以利用两角和与差的三角函数求解.

练习册系列答案
相关题目
10.设双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的离心率为e,右顶点为A,点Q(3a,0),若C上存在一点P,使得AP⊥PQ,则( )
| A. | $e∈({1,\sqrt{2}})$ | B. | $e∈({\sqrt{2},\sqrt{3}})$ | C. | $e∈({1,\sqrt{3}})$ | D. | $e∈({\sqrt{2},+∞})$ |
7.F1是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点,点P是双曲线右支上一点,若线段PF1与y轴的交点M恰为PF1的中点,且|OM|=a(O为坐标原点),则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
4.如图,设正方体ABCD-A1B1C1D1的棱长为1,则直线B1C与平面AB1D1所成的角的正弦值是( )

| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
8.满足{a,b}⊆A?{a,b,c,d,e}的集合A的个数是( )
| A. | 2 | B. | 6 | C. | 7 | D. | 8 |
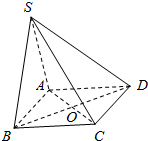 如图,已知四边形ABCD为正方形,SA⊥AB,SA⊥AC,AC与BD的交点为O,AB=2$\sqrt{2}$cm,SC=5cm.
如图,已知四边形ABCD为正方形,SA⊥AB,SA⊥AC,AC与BD的交点为O,AB=2$\sqrt{2}$cm,SC=5cm.