Question

9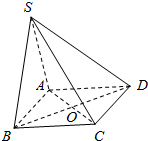．如图，已知四边形ABCD为正方形，SA⊥AB，SA⊥AC，AC与BD的交点为O，AB=2$\sqrt{2}$cm，SC=5cm．
（1）求点S到平面ABCD的距离；
（2）求点S到直线BC的距离；
（3）求异面直线SC与AB所成的角的正切值；
（4）求直线SB与平面ABCD所成的角的正弦值．

Answer 1

分析 （1）由已知得SA⊥平面ABCD，由此能求出S到平面ABCD的距离．
（2）由已知条件利用三垂线定理推导出SB⊥BC，由此能求出点S到直线BC的距离．
（3）由SA⊥平面ABCD，得∠SCA是直线SC与平面ABCD所成角，由此能求出异面直线SC与AB所成的角的正切值．
（4）由SA⊥平面ABCD，得∠SBA是直线SB与平面ABCD所成角，由此能求出异面直线SB与AB所成的角的正切值．

解答 解：（1）∵四边形ABCD为正方形，SA⊥AB，SA⊥AC，AB∩AC=A，
∴SA⊥平面ABCD，
∵AB=2$\sqrt{2}$cm，SC=5cm，
∴$AC=\sqrt{（2\sqrt{2}）^{2}+（2\sqrt{2}）^{2}}$=4，
∴S到平面ABCD的距离SA=$\sqrt{S{C}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3（cm）．
（2）∵SA⊥平面ABCD，AB⊥BC，
∴SB⊥BC，∴SB是点S到直线BC的距离，
∴点S到直线BC的距离SB=$\sqrt{S{A}^{2}+A{B}^{2}}$=$\sqrt{9+8}$=$\sqrt{17}$（cm）．
（3）∵SA⊥平面ABCD，∴∠SCA是直线SC与平面ABCD所成角，
∵SA=3，AC=4，
∴tan∠SCA=$\frac{SA}{AC}$=$\frac{3}{4}$，
∴异面直线SC与AB所成的角的正切值为$\frac{3}{4}$．
（4）SA⊥平面ABCD，∴∠SBA是直线SB与平面ABCD所成角，
∵SA=3，AB=2$\sqrt{2}$，
∴tan∠SBA=$\frac{SA}{AB}$=$\frac{3}{2\sqrt{2}}$=$\frac{3\sqrt{2}}{4}$，
∴异面直线SB与AB所成的角的正切值为$\frac{3\sqrt{2}}{4}$．

点评 本题考查点到平面的距离、异面直线所成角的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．