题目内容
从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是
| A.至少1个白球,都是白球 |
| B.至少1个白球,至少1个红球 |
| C.至少1个白球,都是红球 |
| D.恰好1个白球,恰好2个白球 |
D
解析试题分析:对于A是不互斥的事件,对于B也是不互斥的事件,对于C是对立的事件,只有D是互斥而不对立的两个事件,故选D.
考点:本题考查了互斥事件、对立事件的概念
点评:弄清事件的所有基本事件的基本情况,然后根据互斥事件、对立事件的概念处理即可。

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
投掷两颗骰子,其向上的点数分别为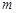 和
和 ,则复数
,则复数 为纯虚数的概率为( )
为纯虚数的概率为( )
A. | B. | C. | D. |
如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子(假设它落在正方形区域内任何位置的机会均等),它落在阴影区域内的概率为 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
A. | B. | C. | D.无法计算 |
从1,2,3,4四个数字中任取两个数求和,则和恰为偶数的概率是( )
A. | B. | C. | D. |
若以连续掷两次骰子分别得到的点数 作为点
作为点 的坐标,则点
的坐标,则点 落在圆
落在圆 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
如图,某人向圆内投镖,如果他每次都投入圆内,那么他投中正方形区域的概率为
A. | B. | C. | D. |


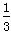


 ,则“出现1点或2点”的概率为( ).
,则“出现1点或2点”的概率为( ).
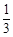

 中,当解释变量 x 每增加一个单位时,预报变量
中,当解释变量 x 每增加一个单位时,预报变量 增加0.1个单位 ( )
增加0.1个单位 ( )