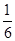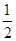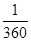题目内容
如图,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子(假设它落在正方形区域内任何位置的机会均等),它落在阴影区域内的概率为 ,则阴影区域的面积为( )
,则阴影区域的面积为( )
A. | B. | C. | D.无法计算 |
B
解析试题分析:由几何概型概率的计算公式的 =
= ,所以阴影区域的面积为
,所以阴影区域的面积为 ×4=
×4= ,故选B。
,故选B。
考点:本题主要考查几何概型概率的计算。
点评:简单题,阴影面积与正方形面积之比就是题中概率。

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
设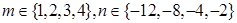 ,则函数
,则函数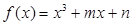 在区间
在区间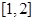 上有零点的概率是( )
上有零点的概率是( )
A.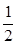 | B.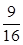 | C.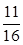 | D. |
从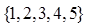 中随机选取一个数为
中随机选取一个数为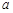 ,从
,从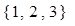 中随机选取一个数为
中随机选取一个数为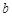 ,则
,则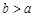 的概率是 ( )
的概率是 ( )
A.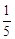 | B.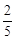 | C.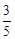 | D.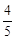 |
从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是
| A.至少1个白球,都是白球 |
| B.至少1个白球,至少1个红球 |
| C.至少1个白球,都是红球 |
| D.恰好1个白球,恰好2个白球 |
口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.7 | D.0.3 |
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
下列说法一定正确的是( )
| A.一名篮球运动员,号称“百发百中”,若罚球三次,不会出现三投都不中的情况 |
B.一枚硬币掷一次得到正面的概率是 ,那么掷两次一定会出现一次正面的情况 ,那么掷两次一定会出现一次正面的情况 |
| C.如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元 |
| D.随机事件发生的概率与试验次数无关 |