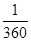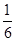题目内容
抛掷一骰子,观察出现的点数,设事件A为“出现1点”,事件B为“出现2点”.已知P(A)=P(B)= ,则“出现1点或2点”的概率为( ).
,则“出现1点或2点”的概率为( ).
A. | B.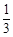 | C. | D. |
B
解析试题分析:因为抛掷一骰子,观察出现的点数共有6种,那么设事件A为“出现1点”,概率为1:6,而事件B为“出现2点”的概率为1:6,那么可知“出现1点或2点”表示的为事件A,B的互斥事件的概率的和,因此为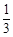 ,选B.
,选B.
考点:本试题考查了古典概型的概率的计算。
点评:根据已知题意确定出事件A,B是互斥事件,那么结合互斥事件的概率的加法公式可知,抛掷一枚骰子,出现任何一点的概率都是1:6,那么可知所求的概率值,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设随机变量X~N(0,1),已知 ,则
,则 ( )
( )
| A.0.025 | B.0.050 |
| C.0.950 | D.0.975 |
从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是
| A.至少1个白球,都是白球 |
| B.至少1个白球,至少1个红球 |
| C.至少1个白球,都是红球 |
| D.恰好1个白球,恰好2个白球 |
 和
和 ,两个零件是否加工为一等品相互独立,则这两个零件中恰好有一个一等品的概率为( )
,两个零件是否加工为一等品相互独立,则这两个零件中恰好有一个一等品的概率为( )



 的分布列如下表,随机变量
的分布列如下表,随机变量 ,则
,则 的值为( )
的值为( )
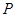


 C.
C.
 ,则
,则 的概率为
的概率为