题目内容
如图,某人向圆内投镖,如果他每次都投入圆内,那么他投中正方形区域的概率为
A. | B. | C. | D. |
A
解析试题分析:设圆的半径为r,则正方形的周长为 ,所以投中正方形区域的概率
,所以投中正方形区域的概率 。
。
考点:几何概型。
点评:本题考查的知识点是几何概型,几何概型的概率计算公式中的“几何度量”,可以为线段长度、面积、体积、角度等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是
| A.至少1个白球,都是白球 |
| B.至少1个白球,至少1个红球 |
| C.至少1个白球,都是红球 |
| D.恰好1个白球,恰好2个白球 |
设随机变量 ~
~ ,又
,又 ,则
,则 和
和 的值分别是( )
的值分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
已知 是
是 所在平面内一点,
所在平面内一点, ,现将一粒
,现将一粒
黄豆随机撒在 内,则黄豆落在
内,则黄豆落在 内的概率是( )
内的概率是( )
A. | B. | C. | D. |
 的分布列如下表,随机变量
的分布列如下表,随机变量 ,则
,则 的值为( )
的值为( )
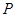


 C.
C.

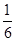



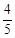



 是区间
是区间 的任意值,把事件“函数
的任意值,把事件“函数 在
在


