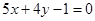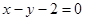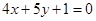题目内容
已知函数f(x)= ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)当a≤0时,求f(x)的单调区间。
 ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R).(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)当a≤0时,求f(x)的单调区间。
(1)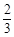 ;(2)当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增.
;(2)当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增.
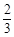 ;(2)当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增.
;(2)当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增.试题分析:(1)因为f(x)=
 ax2-(2a+1)x+2lnx,所以f′(x)=ax?(2a+1)+
ax2-(2a+1)x+2lnx,所以f′(x)=ax?(2a+1)+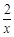 .因为曲线y=f(x)在x=1和x=3处的切线互相平行,所以f′(1)=f′(3).由此能求出实数a.
.因为曲线y=f(x)在x=1和x=3处的切线互相平行,所以f′(1)=f′(3).由此能求出实数a.(2)因为函数f(x)的定义域是(0,+∞),且f′(x)=
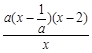 ,再由实数a的取值范围进行分类讨论,能够求出f(x)的单调区间.
,再由实数a的取值范围进行分类讨论,能够求出f(x)的单调区间.试题解析:函数f(x)的定义域为(0,+∞)
∵f ' (x)=ax-(2a+1)+
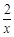
(1)由已知函数f ' (1)=f ' (3)
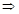 a-(2a+1)+2=3a-(2a+1)+
a-(2a+1)+2=3a-(2a+1)+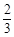
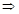 a=
a=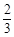 6分
6分(2)f ' (x)=
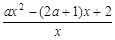 =
=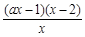 (x∈(0,+∞)) 8分
(x∈(0,+∞)) 8分①当a=0时,f ' (x)=
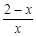 ,由f ' (x)>0得0<x<2,由f ' (x)<0得x>2
,由f ' (x)>0得0<x<2,由f ' (x)<0得x>2∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减 10分
②当a<0时,由f ' (x)=
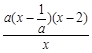 =0的x1=
=0的x1=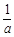 (舍去),x2=2,由f ' (x)>0的0<x<2,由f ' (x)<0的x>2
(舍去),x2=2,由f ' (x)>0的0<x<2,由f ' (x)<0的x>2∴f(x)在(0,2)上单调递增,在(2,+∞)上单调递减 12分
综上:当a≤0时,f(x)在(0,2)上单调递增,在(2,+∞)上单调递增 13分

练习册系列答案
相关题目
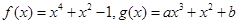 (
(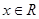 ),其中
),其中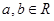 .
.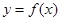 与
与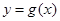 在点
在点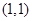 处相交且有相同的切线,求
处相交且有相同的切线,求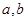 的值;
的值;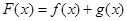 ,若对于任意的
,若对于任意的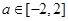 ,函数
,函数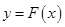 在区间
在区间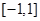 上的值恒为负数,求
上的值恒为负数,求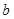 的取值范围.
的取值范围.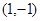 且与曲线
且与曲线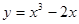 相切的直线方程为( )
相切的直线方程为( )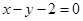 或
或