题目内容
已知函数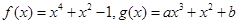 (
(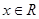 ),其中
),其中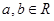 .
.
(1)若曲线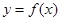 与
与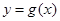 在点
在点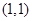 处相交且有相同的切线,求
处相交且有相同的切线,求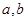 的值;
的值;
(2)设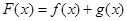 ,若对于任意的
,若对于任意的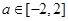 ,函数
,函数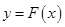 在区间
在区间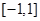 上的值恒为负数,求
上的值恒为负数,求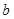 的取值范围.
的取值范围.
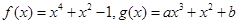 (
(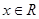 ),其中
),其中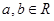 .
.(1)若曲线
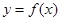 与
与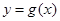 在点
在点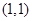 处相交且有相同的切线,求
处相交且有相同的切线,求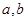 的值;
的值;(2)设
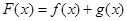 ,若对于任意的
,若对于任意的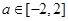 ,函数
,函数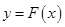 在区间
在区间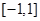 上的值恒为负数,求
上的值恒为负数,求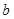 的取值范围.
的取值范围.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)确定
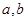 的值,需要确定两个独立的条件,依题意,首先
的值,需要确定两个独立的条件,依题意,首先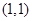 在曲线
在曲线 上,代入得关于
上,代入得关于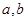 的方程,再
的方程,再 ,又得关于
,又得关于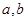 的方程,联立求
的方程,联立求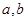 ;(2)多元函数,可采取选取主元法.由题意知,对任意的
;(2)多元函数,可采取选取主元法.由题意知,对任意的 ,在
,在 上
上 恒成立,首先采取参变分离法,变形为
恒成立,首先采取参变分离法,变形为 恒成立,左边看作自变量为
恒成立,左边看作自变量为 的函数
的函数
 ,
, ,只需求函数
,只需求函数 的最大值,且
的最大值,且 .
.试题解析:(1)
 ,切线斜率
,切线斜率 ,
,由题知
 ,即
,即 ,解得
,解得 .
.(2)由题知对任意的
 ,在
,在 上
上 恒成立,
恒成立,即
 恒成立.
恒成立.设
 ,则
,则
 ,
,令
 ,则对任意的
,则对任意的 ,恒有
,恒有 ,则恒有
,则恒有
当
 时,
时, ,函数
,函数 单调递减,
单调递减,当
 时,
时, ,函数
,函数 单调递增。
单调递增。 =4,
=4,所以
 ,即
,即

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
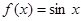 .
.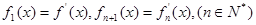 ,求
,求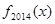 的解析式;
的解析式;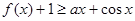 在
在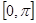 上恒成立,求实数
上恒成立,求实数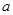 的取值范围;
的取值范围;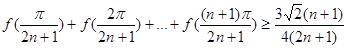 .
.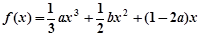 ,
,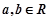 ,
,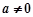 ,
, 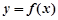 与
与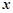 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数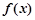 的极小值为
的极小值为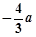 ,求
,求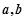 的值;
的值;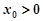 ,且
,且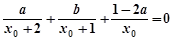 ,
,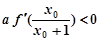 ; ②求证:
; ②求证: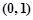 上存在极值点.
上存在极值点. ax2-(2a+1)x+2lnx(a∈R).
ax2-(2a+1)x+2lnx(a∈R). 在点
在点 处的切线平行于x轴,则k= ( )
处的切线平行于x轴,则k= ( )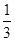 ax3+
ax3+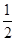 bx2+cx(c<0),其图象在点A(1,0)处的切线的斜率为0,则f(x)的单调递增区间是________.
bx2+cx(c<0),其图象在点A(1,0)处的切线的斜率为0,则f(x)的单调递增区间是________.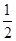 x+b是曲线y=lnx(x>0)的一条切线,则实数b=________.
x+b是曲线y=lnx(x>0)的一条切线,则实数b=________.