题目内容
已知f(α)=
.
(Ⅰ)化简f(α);
(Ⅱ)若f(α)=
-cosα,且α∈(0,π),求sinα-cosα的值.
sin(2π-α)cos(π+α)cos(
| ||
sin(-π-α)sin(
|
(Ⅰ)化简f(α);
(Ⅱ)若f(α)=
| 4 |
| 5 |
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:(Ⅰ)根据三角函数的诱导公式进行化简f(α);
(Ⅱ)根据同角的三角函数关系式进行求解.
(Ⅱ)根据同角的三角函数关系式进行求解.
解答:
解:(Ⅰ) f(α)=
=
=sinα
(Ⅱ)由(Ⅰ)得f(α)=sinα,
∴sinα=
-cosα,即sinα+cosα=
,
两边平方得1+2sinαcosα=
,
∴sinαcosα=-
<0
又α∈(0,π),则α∈(
,π),
∴sinα-cosα>0
由(sinα-cosα)2=1-2sinαcosα=1+
=
,
故sinα-cosα=
sin(-α)(-cosα)cos(
| ||
sin(π-α)sin(
|
| -sinα(-cosα)sinα |
| sinαcosα |
(Ⅱ)由(Ⅰ)得f(α)=sinα,
∴sinα=
| 4 |
| 5 |
| 4 |
| 5 |
两边平方得1+2sinαcosα=
| 16 |
| 25 |
∴sinαcosα=-
| 9 |
| 50 |
又α∈(0,π),则α∈(
| π |
| 2 |
∴sinα-cosα>0
由(sinα-cosα)2=1-2sinαcosα=1+
| 9 |
| 25 |
| 34 |
| 25 |
故sinα-cosα=
| ||
| 5 |
点评:本题主要考查三角函数值的化简和求值,利用三角函数的诱导公式以及同角的三角函数的关系式是解决本题的关键.

练习册系列答案
相关题目
下列大小关系,正确的是( )
| A、23.4<24.3 |
| B、log20.8>log21.8 |
| C、1.53>1.63 |
| D、1.70.3<0.93.1 |
若a,b,c是△ABC的三边,且
>1,则△ABC一定是( )
| c | ||
|
| A、直角三角形 |
| B、等边三角形 |
| C、锐角三角形 |
| D、钝角三角形 |
“x=-1”是“x2=1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知命题p:“将函数y=sin(2x+θ)的图象沿x轴向右平移
个单位后,得到一个关于y轴对称的图象”,命题q:“θ=kπ+
(k∈Z)”则p是q的 ( )条件.
| π |
| 16 |
| 5π |
| 8 |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
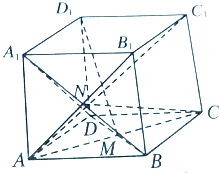 如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.
如图,在正方形ABCD-A1B1C1D1中,M,N分别为正方形ABCD和AA1B1B的重心.