题目内容

21、已知函数f （x）的定义域是（0，+∞），满足f（2）=1，且对于定义域内任意x，y都有f（xy）=f（x）+f（y）成立，那么f（1）+f（4）=
2
．
分析：由f（1）=f（1×1）=f（1）+f（1）=2f（1），可得 f（1）=0，同理可得 f（4）=2，从而得到所求．
解答：解：f（1）=f（1×1）=f（1）+f（1）=2f（1），
∴f（1）=0．
f（4）=f（2×2）=f（2）+f（2）=2，
∴f（1）+f（4）=0+2=2，
故答案为2．
点评：本题考查抽象函数的应用，求出f（1）=0 和f（4）=2，是解题的关键．
练习册系列答案
相关题目
已知函数f（x）的定义域为[-1，5]，部分对应值如下表．
x -1 0 2 4 5
f（x） 1 2 0 2 1
f（x）的导函数y=f′（x）的图象如图所示．下列关于函数f（x）的命题：
①函数f（x）在[0，1]上是减函数；
②如果当x∈[-1，t]时，f（x）最大值是2，那么t的最大值为4；
③函数y=f（x）-a有4个零点，则1≤a＜2；
④已知（a，b）是y=
2013
f(x)
的一个单调递减区间，则b-a的最大值为2．
其中真命题的个数是
3
3
．
已知函数f（x）的定义域为A，若其值域也为A，则称区间A为f（x）的保值区间．若g（x）=-x+m+ex的保值区间为[0，+∞），则m的值为（　　）
已知函数f（x）的定义域是R，若f（x）是奇函数，0≤x＜1时，f（x）=
1
2
x，且满足f（x+2）=f（x）．
（1）写出f（x）的周期．
（2）求-1≤x≤0时，f（x）的解析式．
（3）求1＜x＜3时，f（x）的解析式．
（4）求使f（x）=-
1
2
成立所有x．
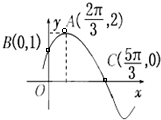
已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（　　）
精英家教网
A、f（x）=2sin（
x
2
+
π
6
）
B、f（x）=
2
sin（4x+
π
4
）
C、f（x）=2sin（
x
2
-
π
6
）
D、f（x）=
2
sin（4x-
π
4
）
已知函数f（x）的定义域为[-3，+∞），部分函数值如表所示，其导函数的图象如图所示，若正数a，b满足f（2a+b）＜1，则
b+2
a+2
的取值范围是
（
2
5
，4）
（
2
5
，4）
；
x -3 0 6
f（x） 1 -1 1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网