Question

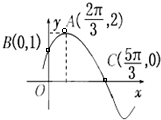
已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（　　）

• A、f（x）=2sin（

  x

  2

  +

  π

  6

  ）
• B、f（x）=

  2

  sin（4x+

  π

  4

  ）
• C、f（x）=2sin（

  x

  2

  -

  π

  6

  ）
• D、f（x）=

  2

  sin（4x-

  π

  4

  ）

Answer 1

分析：观察四个选项，此是要建立一个三角函数模型且没有常数项即y=Asin（ωx+φ），由图可以看出A=2，周期的四分之一为π，再由点（

2π

3

，2），求出φ即得

解答：解：由题意可令函数模型为y=Asin（ωx+φ），由图形知A=2，T=4π，可得ω=

1

2

故可得y=2sin（

1

2

x+φ），
将点（

2π

3

，2）代入得sin（

1

2

×

2π

3

+φ）=1，故有

π

3

+φ=

π

2

∴φ=

π

6

所求函数的解析式为f（x）=2sin（

x

2

+

π

6

）
故选A

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，是三角函数里的看图求解题，求解的关键是求φ，代入最值点求φ是最好的选择，如果不知道最值点的坐标，代入其它点时一定要注意此点是上升图象上的点还是下降图象上的点．