题目内容
已知f（x）为定义在R上的可导函数，且f（x）＜f′（x），对任意x∈R恒成立，则（ ）
| A、f（2）＞e2f（0），f（2012）＞e2012f（0） |
| B、f（2）＜e2f（0），f（2012）＞e2012f（0） |
| C、f（2）＞e2f（0），f（2012）＜e2012f（0） |
| D、f（2）＜e2f（0），f（2012）＜e2012f（0） |
考点：导数的运算
专题：导数的综合应用
分析：构造函数g（x）=
，利用导数研究其单调性即可得出．
| f(x) |
| ex |
解答：
解：令g（x）=
，则g′(x)=
=
＞0，
∴函数g（x）在R上单调递增，
∴g（2）＞g（0），g（2012）＞g（0），
∴
＞
，
＞
，
化为f（2）＞e2f（0），f（2012）＞e2012f（0）．
故选：A．
| f(x) |
| ex |
| f′(x)ex-f(x)ex |
| e2x |
| f′(x)-f(x) |
| ex |
∴函数g（x）在R上单调递增，
∴g（2）＞g（0），g（2012）＞g（0），
∴
| f(2) |
| e2 |
| f(0) |
| e0 |
| f(2012) |
| e2012 |
| f(0) |
| e0 |
化为f（2）＞e2f（0），f（2012）＞e2012f（0）．
故选：A．
点评：本题考查了通过构造函数利用导数研究其单调性解决问题的方法，考查了推理能力，属于中档题．
练习册系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
若函数y=x2+bx+3在（-∞，1]上是单调递减函数，则有（ ）
| A、b≥2 | B、b≤2 |
| C、b≥-2 | D、b≤-2 |
若集合M={x|y=
}，N={y|y=x2-2，x∈R}，则M∩N=（ ）
| x |
| A、[0，+∞） |
| B、[-2，+∞） |
| C、∅ |
| D、[-2，0） |
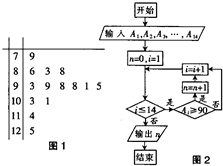如图1是某高三学生14次数学考试成绩的茎叶图，现将该14个数据依次记为A1，A2，…A14，并输入如图2所示的一个算法流程图，那么该算法流程图运行结束时输出的n值是（ ）| A、9 | B、10 | C、11 | D、12 |
设变量x，y满足约束条件
，则z=4x+3y的最大值是（ ）
|
| A、7 | B、8 | C、9 | D、10 |