题目内容
已知f(x)=alnx-b(x-1)对任意的x>0恒有f(x)≤0成立,
(1)求正数a与b的关系;
(2)若a=1,设g(x)=m
+n(m,n∈R),若lnx≤g(x)≤b(x-1)对任意x>0恒成立,求函数g(x)的解析式;
(3)证明:n!>e 2n-4
(n∈N,n≥2)
(1)求正数a与b的关系;
(2)若a=1,设g(x)=m
| x |
(3)证明:n!>e 2n-4
| n |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)根据题意易判断函数在x=1处取得最大值,则f′(1)=0,从而可得正数a与b的关系为a=b;
(2)根据a=1,将不等式lnx≤g(x)≤b(x-1)化为lnx<m
+n<x-1,根据不等式的性质将不等式转化即可得到m=n=2,从而求出函数g(x)的解析式;
(3)根据(2)中结论lnx≤2(
-1)可得ln
≤
-2=
-2=4(
-
)-2,根据对数加法运算性质可得ln
<4[(
-
)+(
-
)+…+(
-
)]-2n=4
-2n.化简即可得到不等式n!>e 2n-4
.
(2)根据a=1,将不等式lnx≤g(x)≤b(x-1)化为lnx<m
| x |
(3)根据(2)中结论lnx≤2(
| x |
| 1 |
| k |
| 2 | ||
|
| 4 | ||
2
|
| k |
| k-1 |
| 1 |
| n! |
| n |
| n-1 |
| n-1 |
| n-2 |
| 1 |
| 0 |
| n |
| n |
解答:
解:(1)∵f(x)=alnx-b(x-1),
∴f(1)=0.
又∵对任意的x>0恒有f(x)≤0成立,
∴函数在x=1处取得最大值.
∵f′(x)=
-b=
.
∴f′(1)=0.
∴a=b.
又∵a>0,
∴f(x)在x=1处取得极大值,符合题意.
∴正数a与b的关系为a=b.
(2)∵a=1,
∴b=1.
∴不等式lnx≤g(x)≤b(x-1)可化为
lnx≤m
≤x-1.
令x=1,则0≤m+n≤0.
∴m+n=0.
∴m
-m≤x-1.
∴x-m
+m-1≥0
即(
-
)2-
+m-1≥0对?x>0恒成立.
∴-
+m-1=-(
-1)2≥0,
∴m=2.
∴函数g(x)=2(
-1).
(3)由(2)知,
ln
≤
-2=
-2=4(
-
)-2.
∴ln
<4[(
-
)+(
-
)+…+(
-
)]-2n=4
-2n.
即lnn!>2n-4
(n∈N,n≥2).
∴n!>e 2n-4
(n∈N,n≥2).
∴f(1)=0.
又∵对任意的x>0恒有f(x)≤0成立,
∴函数在x=1处取得最大值.
∵f′(x)=
| a |
| x |
| a-bx |
| x |
∴f′(1)=0.
∴a=b.
又∵a>0,
∴f(x)在x=1处取得极大值,符合题意.
∴正数a与b的关系为a=b.
(2)∵a=1,
∴b=1.
∴不等式lnx≤g(x)≤b(x-1)可化为
lnx≤m
| x |
令x=1,则0≤m+n≤0.
∴m+n=0.
∴m
| x |
∴x-m
| x |
即(
| x |
| m |
| 2 |
| m2 |
| 4 |
∴-
| m2 |
| 4 |
| m |
| 2 |
∴m=2.
∴函数g(x)=2(
| x |
(3)由(2)知,
ln
| 1 |
| k |
| 2 | ||
|
| 4 | ||
2
|
| k |
| k-1 |
∴ln
| 1 |
| n! |
| n |
| n-1 |
| n-1 |
| n-2 |
| 1 |
| 0 |
| n |
即lnn!>2n-4
| n |
∴n!>e 2n-4
| n |
点评:本题考查导数在函数极值,最值中的应用,不等式性质的灵活应用,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
任取m∈(-1,3),则直线(m+1)x+(4-m)y-1=0与x轴、y轴围成的三角形的面积小于
的概率是( )
| 1 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中,说法错误的是( )
| A、“若p,则q”的否命题是:“若¬p,则¬q” |
| B、“?x>2,x2-2x>0”的否定是:“?x≤2,x2-2x≤0” |
| C、“p∧q是真命题”是“p∨q是真命题”的充分不必要条件 |
| D、“若b=0,则函数f(x)=ax2+bx+c是偶函数”的逆命题是真命题 |
如图给出了计算
+
+
+…+
的值的程序框图,其中①②分别是( )
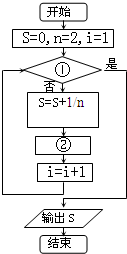
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 60 |

| A、i<30,n=n+2 |
| B、i=30,n=n+2 |
| C、i>30,n=n+2 |
| D、i>30,n=n+1 |