题目内容
6．设a是空间中的一条直线，α是空间中的一个平面，则下列说法正确的是（ ）| A． | 过a一定存在平面β，使得β∥α | |
| B． | 过a一定存在平面β，使得β⊥α | |
| C． | 在平面α内一定不存在直线b，使得a⊥b | |
| D． | 在平面α内一定不存在直线b，使得a∥b |
分析 A．根据面面平行的定义和性质判断．B．利用面面垂直的性质和定义判断．C．根据线面垂直的性质判断．D．根据线面平行的性质判断．
解答 解：A．若a⊥α，则此时α⊥β，∴β∥α不成立，∴A错误．
B．当a⊥α时，有α⊥β成立，∴B正确．
C．不管直线a与平面α的位置关系相交、平行，还是在平面内，都可以在平面α内找到一条直线与直线b垂直，∴C不正确．
D．当a∥α时，根据线面平行的性质可知，在平面α内存在直线b，使得a∥b成立，∴D错误．
故选：C．
点评 本题主要考查空间直线和平面位置关系的判断，要求熟练掌握线面平行和垂直的定义和性质．
练习册系列答案
相关题目
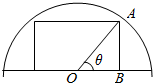如图所示，在一住宅小区里有一块半径为10m的半圆形空地（O为圆心），现准备在这块空地上种植一块矩形草坪，矩形的一边落在半圆的直径上，问角θ为多少度时，矩形草坪面积最大？并求出最大面积．
18．已知圆C：（x-2）2+y2=1，过坐标有原点随机地作一条直线l，则直线l与圆C不相交的概率为（ ）
| A． | $\frac{5}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
