题目内容
15.如图,已知E,F,G,H分别是空间四边形(四条线段首尾相接,且连接点不在同一个平面内,所组成的空间图形叫空间四边形)各边AB,AD,CB,CD上的点,且直线EF和HG交于点P,求证:点B,D,P在同一条直线上.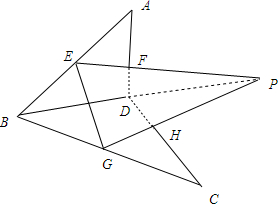
分析 由公理一,得EF?平面ABD,GH?平面CBD,由公理三得P∈BD,由此能证明点B,D,P在同一条直线上..
解答  证明:∵E,F,G,H分别是空间四边形ABCD各边AB,AD,CB,CD上的点,
证明:∵E,F,G,H分别是空间四边形ABCD各边AB,AD,CB,CD上的点,
∴由公理一,得EF?平面ABD,GH?平面CBD,
∵面ABD∩面CBD=BD,直线EF和HG交于点P,
∴由公理三得P∈BD,
∴点B,D,P在同一条直线上..
点评 本题考查三点共线的证明,是基础题,解题时要认真审题,注意公理一和公理三的合理运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
6.设a是空间中的一条直线,α是空间中的一个平面,则下列说法正确的是( )
| A. | 过a一定存在平面β,使得β∥α | |
| B. | 过a一定存在平面β,使得β⊥α | |
| C. | 在平面α内一定不存在直线b,使得a⊥b | |
| D. | 在平面α内一定不存在直线b,使得a∥b |
5.设函数f(x)=$\left\{\begin{array}{l}{x,x≤a}\\{{x}^{2},x>a}\end{array}\right.$,a是R上的常数,若f(x)的值域为R,则a的取值范围为( )
| A. | [-2,-1] | B. | [-1,1] | C. | [0,1] | D. | [1,2] |
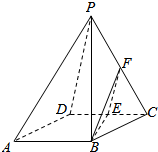 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,E为CD中点,在PC上找一点F,使得PA∥平面BEF.