题目内容
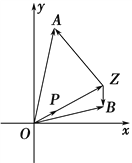
【题目】如图,已知![]() =(2,1),
=(2,1),![]() =(1,7),
=(1,7),![]() =(5,1),设Z是直线OP上的一动点.
=(5,1),设Z是直线OP上的一动点.
(1)求使![]() 取最小值时的
取最小值时的![]() ;
;
(2)对(1)中求出的点Z,求cos∠AZB的值.
【答案】(1)最小值-8,![]() = (4,2)(2)
= (4,2)(2)![]()
【解析】分析:(1)运用向量共线的坐标表示,求得向量ZA,ZB的坐标,由数量积的标准表示,结合二次函数的最值求法,可得最小值,及向量OZ;(2)求得t=2的向量ZA,ZB,以及模的大小,由向量的夹角公式,计算即可得到.
详解:(1)∵Z是直线OP上的一点,∴![]() ∥
∥![]() .
.
设实数t,使![]() =t
=t![]() ,∴
,∴![]() =t(2,1)=(2t,t),
=t(2,1)=(2t,t),
则![]() =
=![]() -
-![]() =(1,7)-(2t,t)=(1-2t,7-t),
=(1,7)-(2t,t)=(1-2t,7-t),
![]() =
=![]() -
-![]() =(5,1)-(2t,t)=(5-2t,1-t).
=(5,1)-(2t,t)=(5-2t,1-t).
∴![]() ·
·![]() =(1-2t)(5-2t)+(7-t)(1-t)=5t2-20t+12=5(t-2)2-8.
=(1-2t)(5-2t)+(7-t)(1-t)=5t2-20t+12=5(t-2)2-8.
当t=2时,![]() ·
·![]() 有最小值-8,此时
有最小值-8,此时![]() =(2t,t)=(4,2).
=(2t,t)=(4,2).
(2)当t=2时,![]() =(1-2t,7-t)=(-3,5),
=(1-2t,7-t)=(-3,5),
|![]() |=
|=![]() ,
,![]() =(5-2t,1-t)=(1,-1),|
=(5-2t,1-t)=(1,-1),|![]() |=
|=![]() .
.
故cos∠AZB=![]() =
=![]() =-
=-![]() =-
=-![]()

练习册系列答案
相关题目