题目内容
已知实数a≠0,函数f(x)=ax(x-2)2 (x∈R)有极大值32.
(1)求实数a的值;
(2)求函数f(x)的单调区间.
解 (1)∵f(x)=ax3-4ax2+4ax,
∴f′(x)=3ax2-8ax+4a=a(3x-2)(x-2).
令f′(x)=0,得x= 或x=2.
或x=2.
∵f(x)=ax(x-2)2 (x∈R)有极大值32,
∴当x= 时,f(x)取得极
时,f(x)取得极 大值32,
大值32,
即 a
a 2=32,∴a=27.
2=32,∴a=27.
(2)由(1)知,f(x)=27x(x-2)2,
∴f′(x)=27(3x-2)(x-2).
令f′(x)>0,则x>2或x< ;
;
令f′(x)<0,则 <x<2.
<x<2.
所以函数f(x)的单调增区间是 ,(2,+∞);
,(2,+∞);
单调减区间是

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在某种新型材料的研制中,实验人员获得了下列一组实验数据:
| x | 1.99 | 3 | 4 | 5.1 | 6.12 |
| y | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
现准备用下列四个函数中的一个 近似地表示这些数据的规律,其中最接近的一个是_____.
近似地表示这些数据的规律,其中最接近的一个是_____.
①y=2x-2 ②y= (x2-1) ③y=log3x ④y=2x-2
(x2-1) ③y=log3x ④y=2x-2
 A+tan B=
A+tan B=
 ,则tan Atan B的值为________.
,则tan Atan B的值为________. )=
)= ,α∈
,α∈ ,则tan α=________.
,则tan α=________. cm.
cm. x3-x2-
x3-x2- x,则f(-a2)与f(-1)的大小关系为 .
x,则f(-a2)与f(-1)的大小关系为 . ,0)时,f(x)=2ax+
,0)时,f(x)=2ax+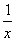 (a为实数).
(a为实数). _______.
_______.