题目内容
19.已知f(x)=x3-4x2+5x-4,则经过点A(2,-2)的曲线f(x)的切线方程为y+2=0或x-y-4=0.分析 设切点坐标为P(a,a3-4a2+5a-4),根据导数的几何意义求出切线的斜率,由点斜式写出切线方程,而点A(2,-2)在切线上,列出关于a的方程,求解a,即可得到曲线的切线方程.
解答 解:设切点坐标为P(a,a3-4a2+5a-4),
∵f(x)=x3-4x2+5x-4,∴f′(x)=3x2-8x+5,
∴切线的斜率为f′(a)=3a2-8a+5,
由点斜式可得切线方程为y-(a3-4a2+5a-4)=(3a2-8a+5)(x-a),①
又根据已知,切线方程过点A(2,-2),
∴-2-(a3-4a2+5a-4)=(3a2-8a+5)(2-a),即a3-5a2+8a-4=0,
∴(a-1)(a2-4a+4)=0,即(a-1)(a-2)2=0,
解得a=1或a=2,
将a=1和a=2代入①可得,切线方程为y+2=0或x-y-4=0,
故经过点A(2,-2)的曲线f(x)的切线方程为y+2=0或x-y-4=0.
故答案为:y+2=0或x-y-4=0.
点评 本题考查了利用导数研究曲线上某点切线方程.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.关于曲线的切线问题,要注意审清题中的条件是“在”点处还是“过”点,是本题问题的易错点.属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4.命题“?n0∈N*,f(n)∈N*且f(n0)>n0的否定形式为( )
| A. | ?n∈N*,f(n)∉N*或f(n)≤n | B. | ?n∈N*,f(n)∉N*且f(n)>n | ||
| C. | ?n0∈N*,f(n0)∉N*且f(n0)>n0 | D. | ?n∈N*,f(n)∉N*且f(n)>n |
11.若变量x,y满足约束条件$\left\{\begin{array}{l}y≤2x\\ x+y≥1\\ y≥-1\end{array}\right.$,则x+2y的最小值是( )
| A. | $-\frac{5}{2}$ | B. | 0 | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
8.在y轴上的截距为2,且与直线y=-3x-4垂直的直线的斜截式方程为( )
| A. | $y=\frac{1}{3}x+2$ | B. | $y=-\frac{1}{3}x-2$ | C. | y=-3x+2 | D. | y=3x-2 |
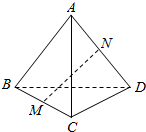 如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.
如图,在四面体ABCD,AB=CD,M,N分别是BC,AD的中点,若AB与CD所成的角的大小为60°,则MN和CD所成的角的大小为30°或60°.