题目内容
已知函数 .
.
(1)当a= 时,求函数f(x)的单调区间和极值;
时,求函数f(x)的单调区间和极值;
(2)当a=2时,试比较f(x)与1的大小;
(3)求证: (n∈N*).
(n∈N*).
解:(1)当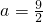 时,
时, ,定义域是(0,+∞).
,定义域是(0,+∞).
∴ =
=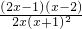 .
.
令f′(x)=0,解得 或x=2.
或x=2.
∵当时, 或x>2时,f′(x)>0;当
或x>2时,f′(x)>0;当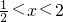 时,f′(x)<0.
时,f′(x)<0.
∴函数f(x)在 或(2,+∞)上单调递增;在
或(2,+∞)上单调递增;在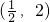 上单调递减.
上单调递减.
∴函数f(x)的极大值是 ,极小值是
,极小值是 .
.
(2)当a=2时,f(x)=lnx+ ,定义域为(0,+∞).
,定义域为(0,+∞).
令h(x)=f(x)-1= ,定义域为(0,+∞).
,定义域为(0,+∞).
∵h′(x)= =
= >0,
>0,
∴h(x)在(0,+∞)是增函数.
①当x>1时,h(x)>h(x)=0,∴f(x)>1.
②当0<x<1时,h(x)<h(1)=0,∴f(x)<1.
③当x=1时,h(1)=0,∴f(x)=1.
(3)根据(2)的结论,
当x>1时, ,即
,即 .
.
令 ,代入得
,代入得 .
.
∴ ,
,
依次取n=1,2,…,n.再相加即可得出:
 .
.
分析:(1)先对f(x)求导,再令f′(x)=0,求出极值点,进而可得出单调区间和极值;
(2)令h(x)=f(x)-1,再求导,利用单调性即可比较出f(x)与1的大小;
(3)利用(2)的结论,即可证出.
点评:熟练掌握利用导数研究函数的单调性与极值是解题的关键.
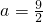 时,
时, ,定义域是(0,+∞).
,定义域是(0,+∞).∴
 =
=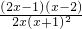 .
.令f′(x)=0,解得
 或x=2.
或x=2.∵当时,
 或x>2时,f′(x)>0;当
或x>2时,f′(x)>0;当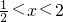 时,f′(x)<0.
时,f′(x)<0.∴函数f(x)在
 或(2,+∞)上单调递增;在
或(2,+∞)上单调递增;在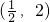 上单调递减.
上单调递减.∴函数f(x)的极大值是
 ,极小值是
,极小值是 .
.(2)当a=2时,f(x)=lnx+
 ,定义域为(0,+∞).
,定义域为(0,+∞).令h(x)=f(x)-1=
 ,定义域为(0,+∞).
,定义域为(0,+∞).∵h′(x)=
 =
= >0,
>0,∴h(x)在(0,+∞)是增函数.
①当x>1时,h(x)>h(x)=0,∴f(x)>1.
②当0<x<1时,h(x)<h(1)=0,∴f(x)<1.
③当x=1时,h(1)=0,∴f(x)=1.
(3)根据(2)的结论,
当x>1时,
 ,即
,即 .
.令
 ,代入得
,代入得 .
.∴
 ,
,依次取n=1,2,…,n.再相加即可得出:
 .
.分析:(1)先对f(x)求导,再令f′(x)=0,求出极值点,进而可得出单调区间和极值;
(2)令h(x)=f(x)-1,再求导,利用单调性即可比较出f(x)与1的大小;
(3)利用(2)的结论,即可证出.
点评:熟练掌握利用导数研究函数的单调性与极值是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 .
. 的极小值;
的极小值; ,x∈[-1,1],求
,x∈[-1,1],求 的最大值F(a).
的最大值F(a). .
. 时,f(x)的值域为[4,6],求a,b的值.
时,f(x)的值域为[4,6],求a,b的值. 函数
函数 .
.