题目内容
已知曲线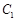 的极坐标方程是
的极坐标方程是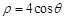 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正方向建立平面直角坐标系,直线的参数方程是:
轴正方向建立平面直角坐标系,直线的参数方程是: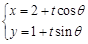 (为参数).
(为参数).
(Ⅰ)求曲线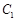 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线与曲线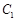 交于
交于 ,
,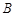 两点,点
两点,点 的直角坐标为
的直角坐标为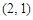 ,若
,若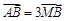 ,求直线的普通方程.
,求直线的普通方程.
(Ⅰ)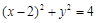 ;(Ⅱ)
;(Ⅱ) 或
或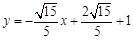 .
.
解析试题分析:(Ⅰ)由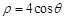 ,得
,得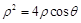 ,
,
∵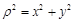 ,
,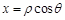
∴曲线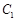 的直角坐标方程是
的直角坐标方程是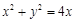 ,即
,即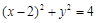 4分
4分
(Ⅱ)设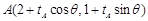 ,
,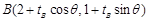
由已知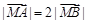 ,注意到
,注意到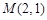 是直线参数方程恒过的定点,
是直线参数方程恒过的定点,
∴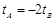 ①
①
联立直线的参数方程与曲线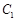 的直角坐标方程得:
的直角坐标方程得: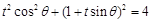 ,
,
整理得: , 6分
, 6分
∴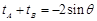 ,
,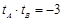 ,与①联立得:
,与①联立得: ,
,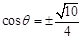
∴直线的参数方程为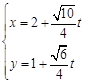 ,(为参数)或
,(为参数)或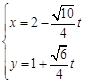 ,(为参数). 8分
,(为参数). 8分
消去参数得的普通方程为 或
或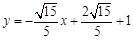 . 10分
. 10分
考点:本题主要考查简单曲线的极坐标方程,直线的参数方程与普通方程的互化。
点评:中档题,极坐标方程与直角坐标方程的互化,主要依据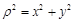 ,
,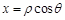 ,
,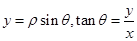 。应用直线的参数方程解题,往往要通过代入方程,得到关于参数的一元二次方程,应用韦达定理。
。应用直线的参数方程解题,往往要通过代入方程,得到关于参数的一元二次方程,应用韦达定理。

练习册系列答案
相关题目
 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为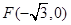 ,右顶点为
,右顶点为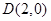 ,设点
,设点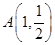 .
.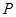 是椭圆上的动点,求线段
是椭圆上的动点,求线段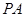 中点
中点 的轨迹方程;
的轨迹方程;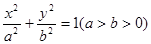 与
与 轴负半轴交于点
轴负半轴交于点 ,
,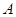 为椭圆第一象限上的点,直线
为椭圆第一象限上的点,直线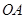 交椭圆于另一点
交椭圆于另一点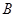 ,椭圆左焦点为
,椭圆左焦点为 ,连接
,连接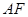 交
交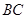 于点D。
于点D。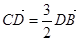 ,求椭圆的离心率;
,求椭圆的离心率; 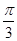 且△ABC的面积为
且△ABC的面积为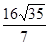 ,求椭圆的标准方程。
,求椭圆的标准方程。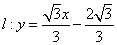 过双曲线
过双曲线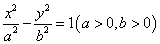 的一个焦点,且与双曲线的一条渐近线平行.
的一个焦点,且与双曲线的一条渐近线平行.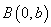 与
与 轴不平行的直线与双曲线相交于不同的两点
轴不平行的直线与双曲线相交于不同的两点 的垂直平分线为
的垂直平分线为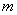 ,求直线
,求直线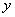 轴上截距的取值范围.
轴上截距的取值范围. (
( ,
,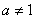 )的图象恒过定点
)的图象恒过定点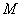 ,椭圆
,椭圆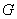 :
: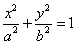 (
(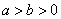 )的左,右焦点分别为
)的左,右焦点分别为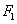 ,
,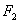 ,直线
,直线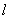 经过点
经过点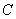 :
: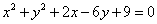 相切.
相切.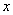 轴上方的交点为
轴上方的交点为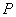 ,且
,且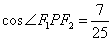 ,求
,求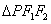 内切圆的方程.
内切圆的方程.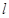 与抛物线
与抛物线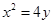 相切于点
相切于点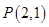 ,且与
,且与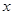 轴交于点
轴交于点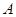 ,
,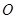 为坐标原点,定点
为坐标原点,定点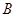 的坐标为
的坐标为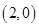 .
. 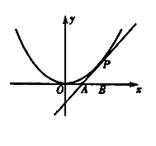
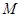 满足
满足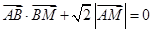 ,求点
,求点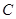 ;
;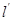 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹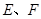 (
(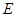 在
在 之间),试求△OBE与△OBF面积之比的取值范围.
之间),试求△OBE与△OBF面积之比的取值范围.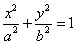 (a>b>0)的离心率为
(a>b>0)的离心率为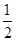 ,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+
,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+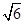 相切.
相切.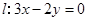 与椭圆在
与椭圆在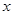 轴上方的一个交点为
轴上方的一个交点为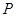 ,
,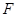 是椭圆的右焦点,试探究以
是椭圆的右焦点,试探究以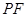 为
为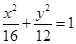 上找一点,使这一点到直线
上找一点,使这一点到直线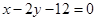 的距离的最小值
的距离的最小值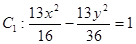 ,点
,点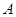 、
、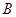 分别为双曲线
分别为双曲线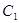 的左、右焦点,动点
的左、右焦点,动点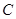 在
在 轴上方.
轴上方.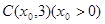 是双曲线的一条渐近线上的点,求以
是双曲线的一条渐近线上的点,求以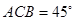 ,求△
,求△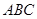 的外接圆的方程;
的外接圆的方程;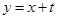 上任取一点
上任取一点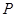 ,从点
,从点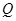 . 问是否存在一个定点
. 问是否存在一个定点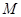 ,恒有
,恒有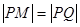 ?请说明理由.
?请说明理由.