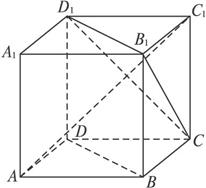
题目内容
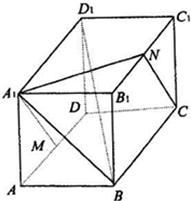
如图,ABCD—A1B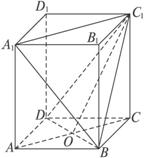
(1)求证:![]() ⊥平面ACC
⊥平面ACC
(2)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的大小.
解法一:(1)证明:∵ABCD—A1B

∴CC1⊥平面ABCD.
∴BD⊥CC1.
∵ABCD是正方形,
∴BD⊥AC.
又∵AC、CC1![]() 平面ACC
平面ACC
∴BD⊥平面ACC
(2)解:设BD与AC相交于O,连结C1O.
∵CC1⊥平面ABCD,BD⊥AC,
∴BD⊥C1O.
∴∠C1OC是二面角C1-BD-C的平面角.
∴∠C1OC=60°.
连结A1B.
∵A
∴∠A
设BC=a,则CO=![]() a,CC1=CO·tan60°=
a,CC1=CO·tan60°=![]() a,A1B=BC1=
a,A1B=BC1=![]() ,A
,A![]() ,
,
在△A1BC1中,由余弦定理得cos∠A![]() ,
,
∴∠A![]() .
.
∴异面直线BC1与AC所成角的大小为arccos![]() .
.
解法二:(1)证明:建立空间直角坐标系D—xyz,如图.
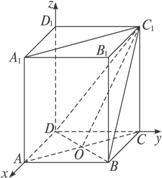
设AD=a,DD1=b,则有D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),C1(0,a,b),
∴![]() =(-a,-a,0),
=(-a,-a,0), ![]() =(-a,a,0),
=(-a,a,0),![]() =(0,0,b).
=(0,0,b).
∴![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0.
=0.
∴BD⊥AC,BD⊥CC1.
又∵AC、CC1![]() 平面ACC
平面ACC
∴BD⊥平面ACC
(2)解:设BD与AC相交于O,连结C1O,则点O坐标为(![]() ,
,![]() ,0),
,0), ![]() =(-
=(-![]() ,
,![]() ,b).
,b).
∵BD·OC1=0,
∴BD⊥C1O.又BD⊥CO,
∴∠C1OC是二面角C1-BD-C的平面角.∴∠C1OC=60°.
∵tan∠C1OC=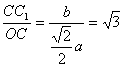 ,∴b=
,∴b=![]() a.
a.
∵![]() =(-a,a,0),
=(-a,a,0), ![]() =(-a,0,b),
=(-a,0,b),
∴cos〈![]() ,
, ![]() 〉=
〉=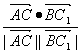 =
=![]() .
.
∴异面直线BC1与AC所成角的大小为arccos![]() .
.

 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=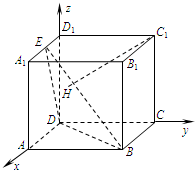 [理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,
[理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点, (2013•崇明县一模)如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD中点.
(2013•崇明县一模)如图,在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.