题目内容
已知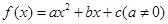 ,且方程
,且方程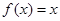 无实数根,下列命题:
无实数根,下列命题:
①方程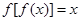 也一定没有实数根;
也一定没有实数根;
②若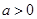 ,则不等式
,则不等式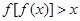 对一切实数
对一切实数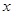 都成立;
都成立;
③若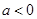 ,则必存在实数
,则必存在实数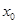 ,使
,使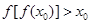
④若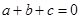 ,则不等式
,则不等式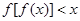 对一切实数
对一切实数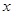 都成立.
都成立.
其中正确命题的序号是 .
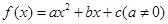 ,且方程
,且方程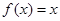 无实数根,下列命题:
无实数根,下列命题:①方程
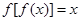 也一定没有实数根;
也一定没有实数根;②若
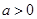 ,则不等式
,则不等式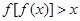 对一切实数
对一切实数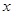 都成立;
都成立;③若
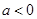 ,则必存在实数
,则必存在实数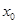 ,使
,使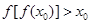
④若
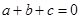 ,则不等式
,则不等式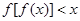 对一切实数
对一切实数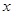 都成立.
都成立.其中正确命题的序号是 .
①②④
试题分析:根据题意,由于
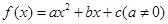 ,且方程
,且方程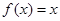 无实数根,
无实数根,则对于①方程
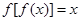 也一定没有实数根;利用反证法可知成立。
也一定没有实数根;利用反证法可知成立。对于②若
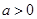 ,则不等式
,则不等式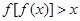 对一切实数
对一切实数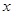 都成立;结合二次函数图象与性质可知成立。
都成立;结合二次函数图象与性质可知成立。对于③若
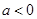 ,则必存在实数
,则必存在实数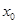 ,使
,使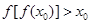 ,不存在,故错误。
,不存在,故错误。对于④若
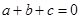 ,则不等式
,则不等式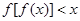 对一切实数
对一切实数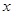 都成立,结合不等式的思想可知成立故答案为①②④
都成立,结合不等式的思想可知成立故答案为①②④点评:主要是考查了函数与方程根的问题的运用,属于基础题。

练习册系列答案
相关题目
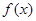 的图象恰好通过
的图象恰好通过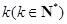 个格点,则称函数
个格点,则称函数 阶格点函数. 给出下列4个函数:
阶格点函数. 给出下列4个函数: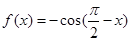 ;②
;②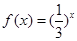 ;③
;③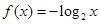 ;④
;④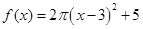 .
. ,曲线
,曲线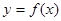 在点
在点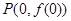 处的切线方程为
处的切线方程为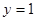
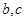 的值
的值 的三条不同切线,求
的三条不同切线,求 的取值范围
的取值范围 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当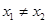 时,
时,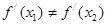
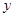 (万元)随投资收益
(万元)随投资收益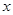 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 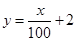 ;②
;②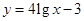 .
.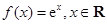 .
. 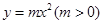 公共点的个数.
公共点的个数. 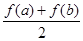 与
与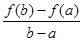 的大小, 并说明理由.
的大小, 并说明理由. 
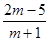 ,则实数m的取值集合是( )
,则实数m的取值集合是( )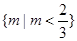
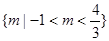
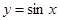 通过坐标变换公式
通过坐标变换公式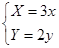 ,变换得到的新曲线为
,变换得到的新曲线为 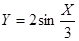
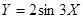

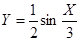
 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当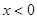 时,不等式
时,不等式 成立,若
成立,若 ,
, ,
,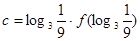 ,则a,b,c间的大小关系是( ).
,则a,b,c间的大小关系是( ). 是( )
是( )