题目内容
函数f（x）=2x+log3x-8的零点有
1
1
个．分析：由题意，判断此函数的零点个数可转化为两个函数y=-2x+8，与y=log3x的交点个数结合两个函数的图象得出两函数图象的交点个数，即可得到原函数零点的个数．
解答：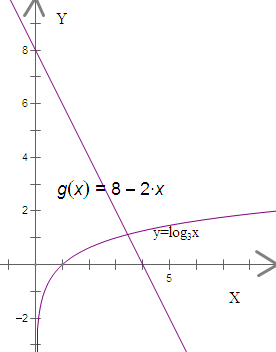
解：函数f（x）=2x+log3x-8的零点与两个函数y=-2x+8与y=log3x的交点个数相同
由右图知，函数y=-2x+8与y=log3x的图象仅有一个交点
故函数f（x）=2x+log3x-8的零点有1个
故答案为 1
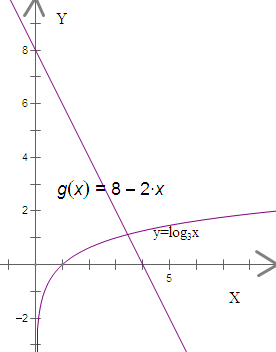解：函数f（x）=2x+log3x-8的零点与两个函数y=-2x+8与y=log3x的交点个数相同由右图知，函数y=-2x+8与y=log3x的图象仅有一个交点
故函数f（x）=2x+log3x-8的零点有1个
故答案为 1
点评：本题考查函数的零点的定义及其个数的判断，解题的关键是理解函数的零点定义，依据定义将求零点个数的问题转化为两个函数交点个数的问题，属于基本题
练习册系列答案
名校课堂系列答案
相关题目
设函数f（x）=
，则满足f（x）=4的x的值是（ ）
|
| A、2 | B、16 |
| C、2或16 | D、-2或16 |