题目内容
已知函数 .
.
(Ⅰ)若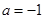 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图象在点(2,f(2))处的切线的倾斜角为
的图象在点(2,f(2))处的切线的倾斜角为 ,对于任意的
,对于任意的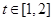 ,函数
,函数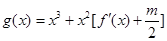
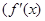 是
是 的导函数)在区间
的导函数)在区间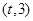 上总不是单调函数,求
上总不是单调函数,求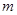 的取值范围;
的取值范围;
(Ⅲ)求证: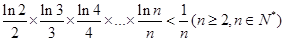 .
.
(Ⅰ) 的单调增区间为
的单调增区间为 ,减区间为
,减区间为
(Ⅱ)  (Ⅲ)先证
(Ⅲ)先证 .
.
解析试题分析:(Ⅰ)当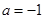 时,
时, .令
.令 得
得 ;令
;令 得
得 ,∴
,∴ 的单调增区间为
的单调增区间为 ,减区间为
,减区间为 .
.
(Ⅱ) ∵ ∴
∴ 得
得 ,
, ,
, ,∴
,∴
∵ 在区间
在区间 上总不是单调函数,且
上总不是单调函数,且 ∴
∴
由题意知:对于任意的 ,
, 恒成立,
恒成立,
所以, ,∴
,∴ . 故
. 故 的取值范围为
的取值范围为 .
.
(Ⅲ)证明如下: 由(Ⅰ)可知
当 时
时 ,即
,即 ,
,
∴ 对一切
对一切 成立.
成立.
∵ ,则有
,则有 ,∴
,∴ .
.  .
.
考点:利用导数研究函数的单调性;利用导数研究曲线上某点切线方程.
点评:本题考查利用函数的导数来求函数的单调区间,已知函数曲线上一点求曲线的切线方程即对函数导数的几何意义的考查,考查求导公式的掌握情况.含参数的数学问题的处理,构造函数求解证明不等式问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 时,函数
时,函数 图象上的点都在
图象上的点都在 所表示的平面区域内,求实数
所表示的平面区域内,求实数 的取值范围.
的取值范围. ,(其中
,(其中 ,
, 是自然对数的底).
是自然对数的底).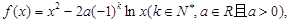
 的单调性;
的单调性;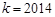 时,关于
时,关于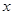 的方程
的方程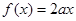 有唯一解,求
有唯一解,求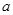 的值;
的值;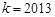 时,证明: 对一切
时,证明: 对一切 ,都有
,都有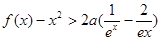 成立.
成立. (
( 为非零常数).
为非零常数). 时,求函数
时,求函数 的最小值;
的最小值; 
 恒成立,求
恒成立,求 (其中
(其中 ),
), .
.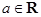 ,函数
,函数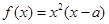 ,若
,若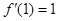 .
.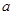 的值并求曲线
的值并求曲线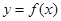 在点
在点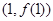 处的切线方程
处的切线方程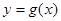 ;
;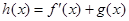 ,求
,求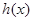 在
在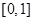 上的最大值与最小值.
上的最大值与最小值.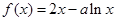 .
. 的单调递增区间;
的单调递增区间;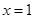 处的切线与直线
处的切线与直线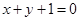 垂直,求证:对任意
垂直,求证:对任意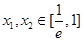 ,都有
,都有 ;
;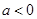 ,对于任意
,对于任意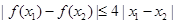 成立,求实数
成立,求实数 的取值范围.
的取值范围. .
.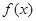 在区间
在区间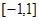 上的最大值;
上的最大值;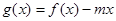 在区间
在区间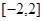 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围.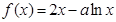 .
.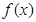 的单调递增区间;
的单调递增区间;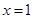 处的切线与直线
处的切线与直线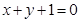 垂直,求证:对任意
垂直,求证:对任意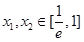 ,都有
,都有 ;
;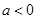 ,对于任意
,对于任意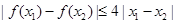 成立,求实数
成立,求实数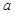 的取值范围.
的取值范围. .
. 在
在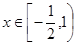 上的最大值为
上的最大值为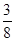 ,求实数
,求实数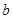 的值;
的值; ,都有
,都有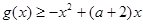 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;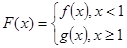 ,对任意给定的正实数
,对任意给定的正实数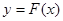 上是否存在两点
上是否存在两点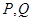 ,使得
,使得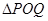 是以
是以 (
( 轴上?请说明理由.
轴上?请说明理由.