题目内容
已知函数 (
( 为非零常数).
为非零常数).
(Ⅰ)当 时,求函数
时,求函数 的最小值;
的最小值;
(Ⅱ)若

 恒成立,求
恒成立,求 的值;
的值;
(Ⅲ)对于 增区间内的三个实数
增区间内的三个实数 (其中
(其中 ),
),
证明: .
.
(Ⅰ)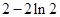 (Ⅱ)
(Ⅱ)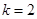 (Ⅲ)由已知得:,
(Ⅲ)由已知得:,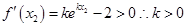
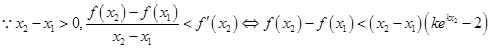
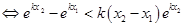
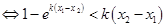
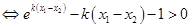 . 设
. 设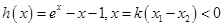
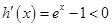 ,
,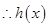 在
在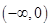 内是减函数,
内是减函数,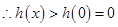 ,即
,即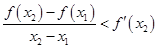 同理
同理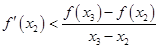 ,∴
,∴
解析试题分析:(Ⅰ)由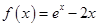 ,得
,得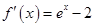 , 1分
, 1分
令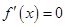 ,得
,得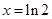 . 当
. 当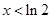 ,
,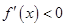 知
知 在
在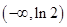 单调递减;
单调递减;
当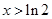 ,
,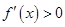 知
知 在
在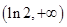 单调递增;
单调递增;
故 的最小值为
的最小值为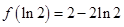 . 4分
. 4分
(Ⅱ)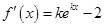 ,当
,当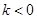 时,
时,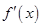 恒小于零,
恒小于零, 单调递减.
单调递减.
当 时,
时,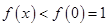 ,不符合题意. 5分
,不符合题意. 5分
对于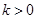 ,由
,由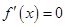 得
得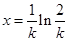
当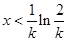 时,
时,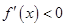 ,∴
,∴ 在
在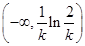 单调递减;
单调递减;
当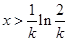 时,
时,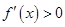 ,∴
,∴ 在
在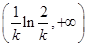 单调递增;
单调递增;
于是 的最小值为
的最小值为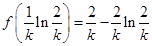 . 7分
. 7分
只需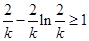 成立即可,构造函数
成立即可,构造函数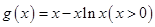 .
.
∵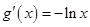 ,∴
,∴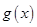 在
在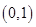 上单调递增,在
上单调递增,在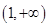 上单调递减,
上单调递减,
则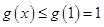 ,仅当
,仅当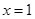 时取得最大值,故
时取得最大值,故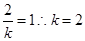 9分
9分
(Ⅲ)由已知得:,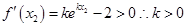
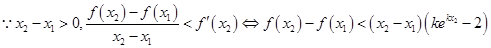
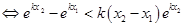
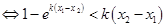
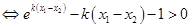 . 设
. 设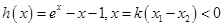
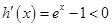 ,
,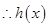 在
在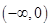 内是减函数,
内是减函数,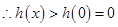 ,即
,即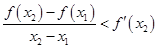 同理
同理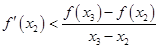 ,∴
,∴
考点:函数单调性最值
点评:求函数最值要结合函数的单调区间确定最值点位置,第二问中不等式恒成立求参数范围常采用分离参数法转化为求函数最值问题,第三问将证明不等式转化为求函数最值

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 ,点
,点 为一定点,直线
为一定点,直线 分别与函数
分别与函数 的图象和
的图象和 轴交于点
轴交于点 ,
, ,记
,记 的面积为
的面积为 .
. 时,求函数
时,求函数 时, 若
时, 若 ,使得
,使得 , 求实数
, 求实数 的取值范围.
的取值范围.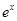 -ln(x+m).
-ln(x+m).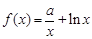 ,
,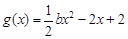 ,
,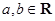
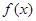 的单调区间;
的单调区间;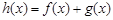 ,当
,当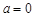 时,
时,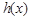 在
在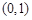 上有且只有一个极值点,求实数
上有且只有一个极值点,求实数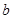 的取值范围;
的取值范围;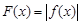 ,证明:存在一条过原点的直线
,证明:存在一条过原点的直线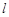 与
与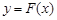 的图象有两个切点
的图象有两个切点 =x+ax2+blnx,曲线y =
=x+ax2+blnx,曲线y =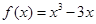
 的单调区间;
的单调区间;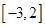 上的最值
上的最值 .
.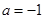 ,求函数
,求函数 的单调区间;
的单调区间;  的图象在点(2,f(2))处的切线的倾斜角为
的图象在点(2,f(2))处的切线的倾斜角为 ,对于任意的
,对于任意的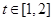 ,函数
,函数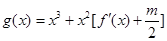
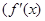 是
是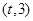 上总不是单调函数,求
上总不是单调函数,求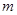 的取值范围;
的取值范围; 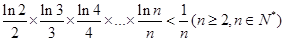 .
.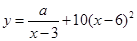 ,其中3<x<6,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
,其中3<x<6,a 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。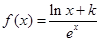 (
(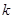 为常数,
为常数,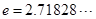 是自然对数的底数),曲线
是自然对数的底数),曲线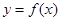 在点
在点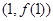 处的切线与
处的切线与 轴平行.
轴平行.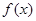 的单调区间;
的单调区间;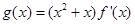 ,其中
,其中 为
为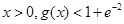 .
.