题目内容
数列{an}是公差不为零的等差数列,且a5,a8,a13是等比数列{bn}相邻的三项,若b2=5,求bn.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:根据所给的三项是等差数列的三项,用第五项和公差表示出三项,根据这三项是等比数列的相邻的三项,写出等式,求出第五项和公差的关系,求出等比数列的公比,写出等比数列的通项.
解答:
解:∵{an}是公差不为零的等差数列,并且a5,a8,a13是等比数列{bn}的相邻三项.
∴(a5+3d)2=a5(a5+8d),
∴a5=
d,
则q=
=
=
,
∴bn=b2•qn-2=5•(
)n-2.
∴(a5+3d)2=a5(a5+8d),
∴a5=
| 9 |
| 2 |
则q=
| a5+3d |
| a5 |
| ||
|
| 5 |
| 3 |
∴bn=b2•qn-2=5•(
| 5 |
| 3 |
点评:本题考查了等差数列的通项公式,考查了等比数列的通项公式与性质,是中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
函数f(x)=
+ln
的零点所在的大致区间是( )
| 2 |
| x |
| 1 |
| x-1 |
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(1,2)与(2,3) |
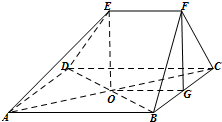 如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.
如图,在多面体ABCDEF中,四边形ABCD是菱形,AC,BD相交于点O,EF∥AB,AB=2EF,平面BCF⊥平面ABCD,BF=CF,点G为BC的中点.