题目内容
设Sn是各项都是正数的等比数列{an} 的前n项和,若 ,则公比q的取值范围是
,则公比q的取值范围是
- A.q>0
- B.0<q≤1
- C.0<q<1
- D.0<q<1或q>1
B
分析:由已知中设Sn是各项都是正数的等比数列{an} 的前n项和,若 ,我们易得到公比q=
,我们易得到公比q=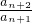 的表达式,进而得到q=
的表达式,进而得到q=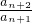 的范围.
的范围.
解答:∵若 ,
,
即Sn+Sn+2≤2Sn+1
即(Sn+1-an+1)+(Sn+1+an+2)≤2Sn+1
即an+2-an+1≤0
即an+2≤an+1
又∵Sn是各项都是正数的等比数列{an}
∴q=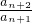 ∈(0,1]
∈(0,1]
故选B
点评:本题考查的知识点是等比数列的性质,其中根据已知条件,将 转化为an+2-an+1≤0,是解答本题的关键.
转化为an+2-an+1≤0,是解答本题的关键.
分析:由已知中设Sn是各项都是正数的等比数列{an} 的前n项和,若
 ,我们易得到公比q=
,我们易得到公比q=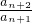 的表达式,进而得到q=
的表达式,进而得到q=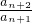 的范围.
的范围.解答:∵若
 ,
,即Sn+Sn+2≤2Sn+1
即(Sn+1-an+1)+(Sn+1+an+2)≤2Sn+1
即an+2-an+1≤0
即an+2≤an+1
又∵Sn是各项都是正数的等比数列{an}
∴q=
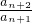 ∈(0,1]
∈(0,1]故选B
点评:本题考查的知识点是等比数列的性质,其中根据已知条件,将
 转化为an+2-an+1≤0,是解答本题的关键.
转化为an+2-an+1≤0,是解答本题的关键. 
练习册系列答案
相关题目
设Sn是各项都是正数的等比数列{an} 的前n项和,若
≤Sn+1,则公比q的取值范围是( )
| Sn+Sn+2 |
| 2 |
| A、q>0 |
| B、0<q≤1 |
| C、0<q<1 |
| D、0<q<1或q>1 |
 ,则公比q的取值范围是( )
,则公比q的取值范围是( ) ,则公比q的取值范围是 .
,则公比q的取值范围是 . ,则公比q的取值范围是 .
,则公比q的取值范围是 .