��Ŀ����
7��ˮ�����ˮ����ʱ����仯������t��ʾʱ�䣬����Ϊ��λ�����Ϊ��㣬�����������ݣ�ijˮ�����ˮ������λ���������ף�����t�Ľ��ƺ�����ϵʽΪV��t��=$\left\{\begin{array}{l}{��-{t}^{2}+14t-40��{e}^{\frac{1}{t}}+60��0��t��10}\\{4��t-10����3t-4��+60��10��t��12}\end{array}\right.$����ˮ�����ˮ��С��60��ʱ�ڳ�Ϊ��ˮ�ڣ���i-1��t��i��ʾ��i�·ݣ�i=1��2��3������12������ͬһ�����ǿ�ˮ�ڵ��·�����5������ �ֶ����ˮ���������С��60ʱx��ȡֵ��Χ��ע��ʵ������xҪȡ�������ɵó����ۣ�
��� �⣺��1����0��t��10ʱ��V��t��=��-t2+14t-40��${e}^{\frac{1}{t}}$+60��60��
�����t2-14t+40��0��
��t��4��t��10����0��t��10����0��t��4��
��10��t��12ʱ��V��t��=4��t-10����3t-41��+50��50��
����ã�t-10����3t-41����0
��10$��t��\frac{41}{3}$��
��10��t��12��
��10��t��12
���ϵã�0��t��4��10��t��12
��֪��ˮ��Ϊ1�¡�2�¡�3�¡�11�¡�12�¹�5���£�
�ʴ�Ϊ��5��
���� ��С����Ҫ���麯��������ʽ�Ȼ���֪ʶ�������ۺ�������ѧ֪ʶ���ʵ�����������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
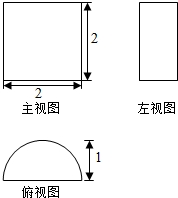
15��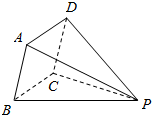 ���ⳤ��Ϊ2������������ABCD�������Σ�������PBCˮƽ���ã������������ĸ���ͼ�����Ϊ��������
���ⳤ��Ϊ2������������ABCD�������Σ�������PBCˮƽ���ã������������ĸ���ͼ�����Ϊ��������
 ���ⳤ��Ϊ2������������ABCD�������Σ�������PBCˮƽ���ã������������ĸ���ͼ�����Ϊ��������
���ⳤ��Ϊ2������������ABCD�������Σ�������PBCˮƽ���ã������������ĸ���ͼ�����Ϊ��������| A�� | $\sqrt{3}$ | B�� | $\frac{\sqrt{3}}{2}$ | C�� | $\frac{4\sqrt{3}}{3}$ | D�� | $\frac{5\sqrt{3}}{3}$ |
12����ͼ�������ĸ��������У����Ǹ��Ե�����ͼ������ͼ������ͼ������ͼ����������ͬ������һ����ͬ�ļ������ǣ�������


| A�� | �٢� | B�� | �ڢ� | C�� | �ڢ� | D�� | �ۢ� |
17������y=ax+3-2��a��0��a��1����ͼ��������A������A��ֱ��$\frac{x}{m}+\frac{y}{n}$=-1�ϣ�m��0��n��0����3m+n����СֵΪ��������
| A�� | 13 | B�� | 16 | C�� | 11+6$\sqrt{2}$ | D�� | 28 |
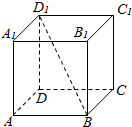 ��ͼ����������ABCD-A1B1C1D1�У���ƽ��aƽ���ڸ����������Խ���BD����ƽ��a�ڸ��������Ͻصõ�ͼ�β�����Ϊ�ڢۢܣ�����ţ�
��ͼ����������ABCD-A1B1C1D1�У���ƽ��aƽ���ڸ����������Խ���BD����ƽ��a�ڸ��������Ͻصõ�ͼ�β�����Ϊ�ڢۢܣ�����ţ�