题目内容
12．如图，下列四个几何体中，它们各自的三视图（主视图、左视图、俯视图）有两个相同，而另一个不同的几何体是（ ）
| A． | ①② | B． | ②③ | C． | ②④ | D． | ③④ |
分析 根据已知中的几何体，分析他们的三视图形状，进而可得答案；
解答 解：①中正方体的三视图均为正方形，不满足条件；
②中圆柱的三视图有两个全等的矩形，一个圆形，满足条件；
③中圆锥的三视图有两个全等的等腰三角形，一个圆形，满足条件；
④中球的三视图均为圆形，不满足条件；
综上所述，满足条件的是②③，
故选：B
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．从装有n+1个球（其中n个白球，1个黑球）的口袋中取出m个球（0＜m≤n，m，n∈N），共有$C_{n+1}^m$种取法．在这$C_{n+1}^m$种取法中，可以分成两类：一类是取出的m个球全部为白球，一类是取出m-1个白球和1个黑球，共有$C_1^0•C_n^m+C_1^1•C_n^{m-1}=C_1^0•C_{n+1}^m$，即有等式：$C_n^m+C_n^{m-1}=C_{n+1}^m$成立．若（1≤k＜m≤n，k，m，n∈N），根据上述思想化简下列式子$C_k^0•C_n^m+C_k^1•C_n^{m-1}+C_k^2•C_n^{m-2}+…+C_k^k•C_n^{m-k}$=的结果为（ ）
| A． | $C_{n+m}^m$ | B． | $C_{n+k}^k$ | C． | $C_{n+k}^m$ | D． | $C_{n+m}^k$ |
20．甲船在湖中B岛的正南A处，AB=3km，甲船以8km/h的速度向正北方向航行，同时乙船自B岛出发，以12km/h的速度向北偏东60°方向驶去，则行驶15分钟时，两船的距离是（ ）
| A． | $\sqrt{7}\;km$ | B． | $\sqrt{13}\;km$ | C． | $\sqrt{19}\;km$ | D． | $\sqrt{10-3\sqrt{3}}\;km$ |
17．
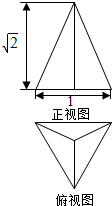已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（ ）
已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（ ）| A． | $\frac{\sqrt{6}}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{6}}{4}$ | D． | $\frac{\sqrt{2}}{4}$ |
4．已知某几何体的三视图如上图所示，则该几何体的体积为（ ）
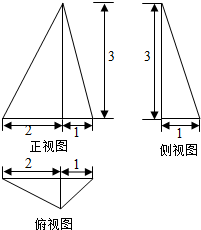
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 3 | D． | 1 |