题目内容
16．一个几何体的三视图如图所示，则该几何体的体积为π；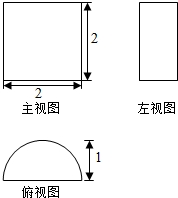
分析 判断几何体的形状，然后求解几何体的体积．
解答 解：由题意可知三视图对应的几何体是圆柱的一半，
该几何体的体积为：$\frac{1}{2}×{1}^{2}×π×2$=π．
故答案为：π．
点评 本题考查三视图对应几何体的体积的求法，考查计算能力．
练习册系列答案
相关题目
4．已知某几何体的三视图如上图所示，则该几何体的体积为（ ）
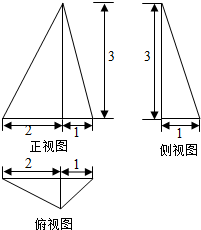
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | 3 | D． | 1 |
8．
一个空间几何体的三视图如图，其中正视图是边长为2的正三角形，俯视图是边长分别为1，2的矩形，则该几何体的侧面积为（ ）
一个空间几何体的三视图如图，其中正视图是边长为2的正三角形，俯视图是边长分别为1，2的矩形，则该几何体的侧面积为（ ）| A． | $\sqrt{3}$+4 | B． | $\sqrt{3}$+6 | C． | 2$\sqrt{3}$+4 | D． | 2$\sqrt{3}$+6 |
5．三棱锥的高为3，底面是边长为3的正三角形，则这个三棱锥的体积是（ ）
| A． | $\frac{27}{4}$ | B． | $\frac{9}{4}$ | C． | $\frac{27\sqrt{3}}{4}$ | D． | $\frac{9\sqrt{3}}{4}$ |
6．已知椭圆E：$\frac{x^2}{4}+\frac{y^2}{2}=1$，直线l交椭圆于A，B两点，若AB的中点坐标为（$\frac{1}{2}$，-1），则l的方程为（ ）
| A． | 2x+y=0 | B． | $x-2y-\frac{5}{2}=0$ | C． | 2x-y-2=0 | D． | $x-4y-\frac{9}{2}=0$ |