题目内容
函数y=lg（3-4x+x2）的定义域为M，求函数f（x）=2x+2-3•4x，x∈M的值域．
考点：函数的值域
专题：计算题,作图题,函数的性质及应用
分析：由题意可得M=（-∞，1）∪（3．+∞）；利用换元法和数形结合求函数的值域．
解答：
解：由3-4x+x2＞0得，
x＞3或x＜1；
则M=（-∞，1）∪（3．+∞）；
又f（x）=2x+2-3•4x，
令t=2x，则0＜t＜2或t＞8．
故y=g（t）=-3t2+4t，
作其函数图象如下，
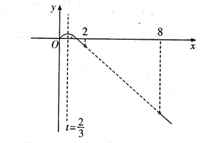
由图象知，g（2）≤g（t）≤g（
）或g（t）＜g（8）；
即-4≤g（t）≤
，或g（t）＜-160；
故函数f（x）的值域为（-∞，-160）∪（-4，
]．
x＞3或x＜1；
则M=（-∞，1）∪（3．+∞）；
又f（x）=2x+2-3•4x，
令t=2x，则0＜t＜2或t＞8．
故y=g（t）=-3t2+4t，
作其函数图象如下，
由图象知，g（2）≤g（t）≤g（
| 2 |
| 3 |
即-4≤g（t）≤
| 4 |
| 3 |
故函数f（x）的值域为（-∞，-160）∪（-4，
| 4 |
| 3 |
点评：本题考查了函数值域的求法．高中函数值域求法有：1、观察法，2、配方法，3、反函数法，4、判别式法；5、换元法，6、数形结合法，7、不等式法，8、分离常数法，9、单调性法，10、利用导数求函数的值域，11、最值法，12、构造法，13、比例法．要根据题意选择．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
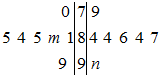如图是2010年“唱响九江”电视歌手大奖赛中，七位专家评委为甲、乙两名选手打出的分数的茎叶图（其中m，n为数字0～9中的一个），去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为a1，a2，则一定有（ ）| A、a1＞a2 |
| B、a2＞a1 |
| C、a1，a2的大小与m的值有关 |
| D、a1，a2的大小与m，n的值都有关 |
设集合A={x|ax＞1，a≤0}，B={x||x|＞1}，若A⊆B，则实数a的取值范围是（ ）
| A、[-1，0] |
| B、[-1，0） |
| C、（-1，0] |
| D、（-∞，-1） |
